Pertanyaan

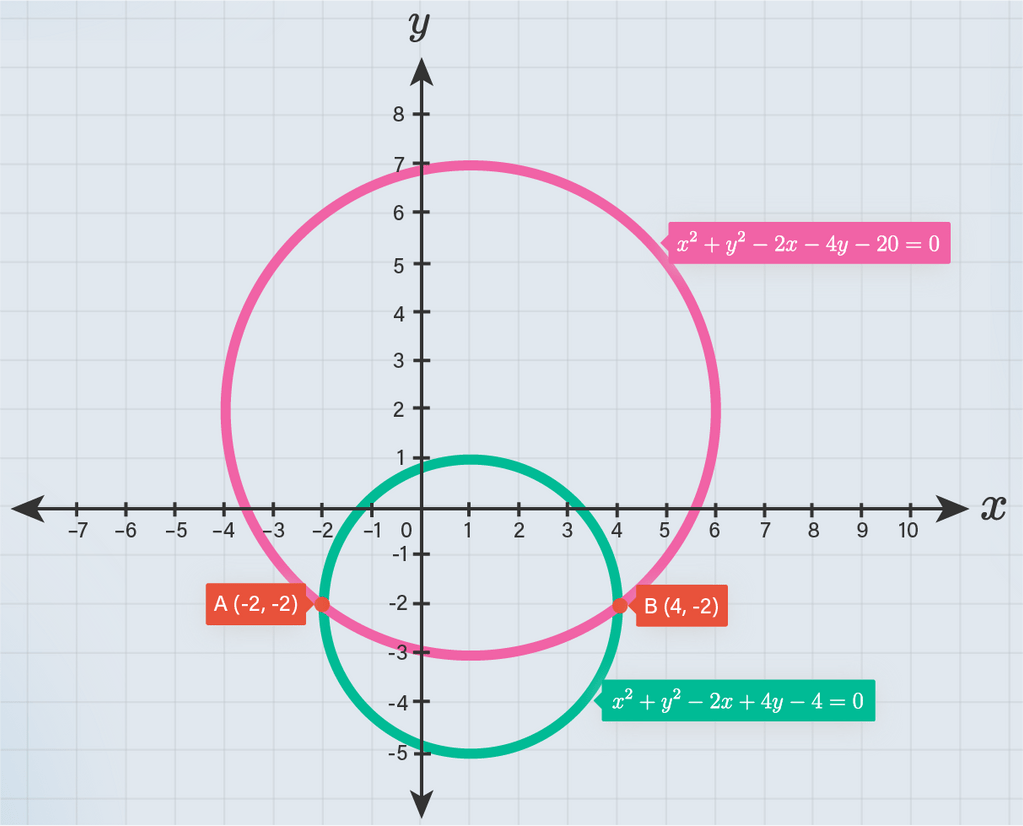
Dua kawat berbentuk lingkaran yang berbeda dipasang sedemikian hingga saling berpotongan. Jika digambarkan dalam bidang koordinat Cartesius, maka kawat pertama merupakan lingkaran yang melalui titik ( − 4 , 2 ) dan ( − 3 , − 1 ) dengan titik pusat berada di garis 3 x − y = 1 .Jika kawat kedua juga digambarkan dalam bidang koordinat Cartesius, maka kawat kedua membentuk lingkaran dengan persamaan x 2 + y 2 − 2 x + 4 y − 4 = 0 . Jika titik potong keduakawat tersebut akan dipasang tali yang membentukgaris lurus, maka persamaan garis lurus tersebut adalah ....

Dua kawat berbentuk lingkaran yang berbeda dipasang sedemikian hingga saling berpotongan. Jika digambarkan dalam bidang koordinat Cartesius, maka kawat pertama merupakan lingkaran yang melalui titik $(- 4, 2)$ dan $(- 3, - 1)$ dengan titik pusat berada di garis $3 x - y = 1$ . Jika kawat kedua juga digambarkan dalam bidang koordinat Cartesius, maka kawat kedua membentuk lingkaran dengan persamaan $x^{2} + y^{2} - 2 x + 4 y - 4 = 0$ . Jika titik potong kedua kawat tersebut akan dipasang tali yang membentuk garis lurus, maka persamaan garis lurus tersebut adalah ....

$x + 2 = 0$
$y + 2 = 0$
$x + y = 2$
$x + y = - 2$
$x = 2 y$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

E. Julianingsih

Master Teacher

Mahasiswa/Alumni Universitas Negeri Yogyakarta

Jawaban terverifikasi

Jawaban

jawaban yang benaradalah B.

jawaban yang benar adalah B.

Pembahasan

Dari persamaan umum lingkaran ( x − a ) 2 + ( y − b ) 2 = r 2 yang berpusat di ( a , b ) maka bisa dilihat bahwa koordinat x titik pusat adalah a dan y titik pusat adalah b . Sehingga variabel x dan y diubah menjadi dan b sebagai berikut: 3 x − y 3 x − y − 1 3 a − b − 1 − b b = = = = = 1 0 0 1 − 3 a 3 a − 1 Selanjutnya mencari nilai dan b dengan cara mensubtitusi titik pusat, titik ( − 4 , 2 ) dan titik ( − 3 , − 1 ) ke persamaan umum lingkaran, sebagai berikut: Untuk ( − 4 , 2 ) ( x − a ) 2 + ( y − b ) 2 ( − 4 − a ) 2 + ( 2 − ( 3 a − 1 )) 2 a 2 + 8 a + 16 + ( − 3 a + 3 ) 2 a 2 + 8 a + 16 + ( 9 a 2 − 18 a + 9 ) 10 a 2 − 10 a + 25 = = = = = r 2 r 2 r 2 r 2 r 2 ⋯ (Persamaan1) Untuk ( − 3 , − 1 ) ( x − a ) 2 + ( y − b ) 2 ( − 3 − a ) 2 + ( − 1 − ( 3 a − 1 )) 2 a 2 + 6 a + 9 + ( − 3 a ) 2 a 2 + 6 a + 9 + 9 a 2 10 a 2 + 6 a + 9 = = = = = r 2 r 2 r 2 r 2 r 2 … (Persamaan2) Eliminasi a 2 dari persamaan (1) dan persamaan (2): 10 a 2 10 a 2 − + 10 a 6 a − 16 a + + + 25 9 16 − 16 a a a = = = = = = r 2 r 2 0 − 16 − 16 − 16 1 − Subtitusi nilai a = 1 ke persamaan b = 3 a − 1 , maka diperoleh: b b = = = 3 a − 1 3 ( 1 ) − 1 2 Subtitusi nilai a = 1 ke persamaan (1) untuk menentukan r 2 , sehingga diperoleh: 10 a 2 − 10 a + 25 10 ( 1 ) 2 − 10 ( 1 ) + 25 10 − 10 + 25 25 = = = = r 2 r 2 r 2 r 2 Subtitusi nilai a = 1 , b = 2 , dan r 2 = 25 ke persamaan umum lingkaran untuk menentukan persamaan lingkaran kawat 1, sehinggadiperoleh: ( x − a ) 2 + ( y − b ) 2 ( x − 1 ) 2 + ( y − 2 ) 2 x 2 − 2 x + 1 + y 2 − 4 y + 4 x 2 + y 2 − 2 x − 4 y + 5 x 2 + y 2 − 2 x − 4 y + 5 − 25 x 2 + y 2 − 2 x − 4 y − 20 = = = = = = r 2 25 25 25 0 0 Titik potong persamaan lingkaran kawat 1 dan kawat 2 dapat ditentukan dengan cara eliminasi dan subtitusi persamaan 1 dan 2. Eliminasi kedua persamaan lingkaran untuk menentukan nilai y : x 2 x 2 + + y 2 y 2 − − 2 x 2 x + − 4 y 4 y 8 y − − + 4 20 16 8 y y y = = = = = = 0 0 0 − 16 8 − 16 − 2 − Subtitusi nilai y = − 2 ke persamaan lingkaran kawat 2 untuk menentukan nilai x : x 2 + y 2 − 2 x + 4 y − 4 x 2 − ( − 2 ) 2 − 2 x + 4 ( − 2 ) − 4 x 2 − 2 x + 4 − 8 − 4 x 2 − 2 x − 8 ( x + 2 ) ( x − 4 ) = = = = = 0 0 0 0 0 x 1 = − 2 atau x 2 = 4 Jadi, kedua lingkaran akan berpotongan di titik ( − 2 , − 2 ) dan ( 4 , − 2 ) . Kedua lingkaran tersebut dapat digambarkan sebagai berikut: Persamaan garis yang melalui kedua titik potong lingkaran tersebut dapat ditentukan dengan cara sebagai berikut: y 2 − y 1 y − y 1 = x 2 − x 1 x − x 1 Oleh karena itu, jawaban yang benaradalah B.

Dari persamaan umum lingkaran $(x - a)^{2} + (y - b)^{2} = r^{2}$ yang berpusat di $(a, b)$ maka bisa dilihat bahwa koordinat $x$ titik pusat adalah $a$ dan $y$ titik pusat adalah $b$ . Sehingga variabel $x$ dan $y$ diubah menjadi $a\;$ dan $b$ sebagai berikut:

$3 x - y 3 x - y - 1 3 a - b - 1 - b b = = = = = 100 1 - 3 a 3 a - 1$

Selanjutnya mencari nilai $a\;$ dan $b$ dengan cara mensubtitusi titik pusat, titik $(- 4, 2)$ dan titik $(- 3, - 1)$ ke persamaan umum lingkaran, sebagai berikut:

Untuk $(- 4, 2)$

$(x - a)^{2} + (y - b)^{2} (- 4 - a)^{2} + (2 - (3 a - 1))^{2} a^{2} + 8 a + 16 + (- 3 a + 3)^{2} a^{2} + 8 a + 16 + (9 a^{2} - 18 a + 9) 10 a^{2} - 10 a + 25 = = = = = r^{2} r^{2} r^{2} r^{2} r^{2} \dots (Persamaan 1)$

Untuk $(- 3, - 1)$

$(x - a)^{2} + (y - b)^{2} (- 3 - a)^{2} + (- 1 - (3 a - 1))^{2} a^{2} + 6 a + 9 + (- 3 a)^{2} a^{2} + 6 a + 9 + 9 a^{2} 10 a^{2} + 6 a + 9 = = = = = r^{2} r^{2} r^{2} r^{2} r^{2} \dots (Persamaan 2)$

Eliminasi $a^{2}$ dari persamaan (1) dan persamaan (2):

$10 a^{2} 10 a^{2} - + 10 a 6 a - 16 a + + + 25916 - 16 a a a = = = = = = r^{2} r^{2} 0 - 16 \frac{- 16}{- 16} 1 -$

Subtitusi nilai $a = 1$ ke persamaan $b = 3 a - 1$ , maka diperoleh:

$b b = = = 3 a - 1 3 (1) - 1 2$

Subtitusi nilai $a = 1$ ke persamaan (1) untuk menentukan $r^{2}$ , sehingga diperoleh:

$10 a^{2} - 10 a + 25 10 (1)^{2} - 10 (1) + 25 10 - 10 + 25 25 = = = = r^{2} r^{2} r^{2} r^{2}$

Subtitusi nilai $a = 1$ , $b = 2$ , dan $r^{2} = 25$ ke persamaan umum lingkaran untuk menentukan persamaan lingkaran kawat 1, sehingga diperoleh:

$(x - a)^{2} + (y - b)^{2} (x - 1)^{2} + (y - 2)^{2} x^{2} - 2 x + 1 + y^{2} - 4 y + 4 x^{2} + y^{2} - 2 x - 4 y + 5 x^{2} + y^{2} - 2 x - 4 y + 5 - 25 x^{2} + y^{2} - 2 x - 4 y - 20 = = = = = = r^{2} 25252500$

Titik potong persamaan lingkaran kawat 1 dan kawat 2 dapat ditentukan dengan cara eliminasi dan subtitusi persamaan 1 dan 2.

Eliminasi kedua persamaan lingkaran untuk menentukan nilai $y$ :

$x^{2} x^{2} + + y^{2} y^{2} - - 2 x 2 x + - 4 y 4 y 8 y - - + 42016 8 y y y = = = = = = 000 - 16 \frac{- 16}{8} - 2 -$

Subtitusi nilai $y = - 2$ ke persamaan lingkaran kawat 2 untuk menentukan nilai $x$ :

$x^{2} + y^{2} - 2 x + 4 y - 4 x^{2} - (- 2)^{2} - 2 x + 4 (- 2) - 4 x^{2} - 2 x + 4 - 8 - 4 x^{2} - 2 x - 8 (x + 2) (x - 4) = = = = = 00000$
$x_{1} = - 2 atau x_{2} = 4$

Jadi, kedua lingkaran akan berpotongan di titik $(- 2, - 2)$ dan $(4, - 2)$ .

Kedua lingkaran tersebut dapat digambarkan sebagai berikut:

Persamaan garis yang melalui kedua titik potong lingkaran tersebut dapat ditentukan dengan cara sebagai berikut:

$\frac{y - y _{1}}{y _{2} - y _{1}} = \frac{x - x _{1}}{x _{2} - x _{1}}$

$table attributes columnalign right center left columnspacing 0px end attributes row cell fraction numerator y plus 2 over denominator negative 2 plus 2 end fraction end cell equals cell fraction numerator x plus 2 over denominator 4 plus 2 end fraction end cell row cell open parentheses y plus 2 close parentheses open parentheses 4 plus 2 close parentheses end cell equals cell open parentheses x plus 2 close parentheses open parentheses negative 2 plus 2 close parentheses end cell row cell open parentheses y plus 2 close parentheses open parentheses 6 close parentheses end cell equals cell open parentheses x plus 2 close parentheses open parentheses 0 close parentheses end cell row cell open parentheses 6 y plus 12 close parentheses end cell equals 0 row cell 6 y end cell equals cell negative 12 end cell row y equals cell fraction numerator negative 12 over denominator 6 end fraction end cell row y equals cell negative 2 end cell row cell bold italic y bold plus bold 2 end cell bold equals bold 0 end table$

Oleh karena itu, jawaban yang benar adalah B.

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Tentukan nilai agar lingkaran dengan persamaan x 2 + y 2 − 2 p x + 6 y + p 2 − 7 = 0 memotong sumbu x di dua titik yang berbeda.

0.0

Jawaban terverifikasi

Agar ada titik persekutuan antara grafik y = 2 x + p dan x 2 + y 2 = 1 , maka nilai haruslah ....

4.8

Jawaban terverifikasi

Selidiki hubungan garis dan lingkaran berikut. a. y = 2 x + 1 dan x 2 + y 2 + 3 x + 5 y − 2 = 0

4.5

Jawaban terverifikasi

Tentukan nilai n agar garis yang diberikan dapat: b. memotong di dua titik yang berlainan, serta x 2 + y 2 = 4 ; y = n x 2 + y 2 + 2 y − 1 = 0 ; y = x − n

5.0

Jawaban terverifikasi

Garis berikut yang memotong lingkaran x 2 + y 2 + 2 x − 2 y − 7 = 0 adalah ....

4.8

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS