Iklan
Pertanyaan
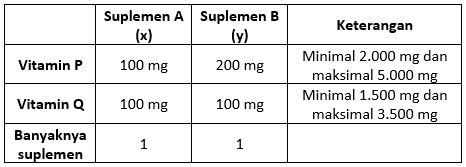
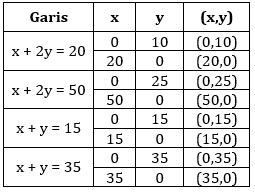
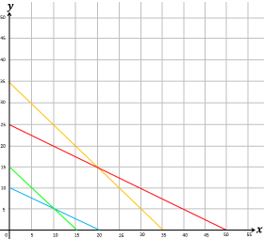
Dodi diharuskan dokter untuk mengkonsumsi dua jenis suplemen setiap bulannya yakni jenis A dan B yang masing-masing suplemen tersebut mengandung vitamin P dan Q. Banyaknya vitamin P yang terkandung dalam suplemen A adalah 100 mg dan 200 mg dalam suplemen B. sedangkan banyaknya vitamin Q yang terkandung dalam suplemen A adalah 100 mg dan 100 mg dalam suplemen B. Dia diharuskan mengkonsumsi vitamin P minimal 2 gram dan maksimal 5 gram, sedangkan vitamin Q minimal 1,5 gram dan maksimal 3,5 gram. Banyaknya suplemen A dan B maksimal yang harus dikonsumsi setiap bulannya adalah ... gram.
Dodi diharuskan dokter untuk mengkonsumsi dua jenis suplemen setiap bulannya yakni jenis A dan B yang masing-masing suplemen tersebut mengandung vitamin P dan Q. Banyaknya vitamin P yang terkandung dalam suplemen A adalah 100 mg dan 200 mg dalam suplemen B. sedangkan banyaknya vitamin Q yang terkandung dalam suplemen A adalah 100 mg dan 100 mg dalam suplemen B. Dia diharuskan mengkonsumsi vitamin P minimal 2 gram dan maksimal 5 gram, sedangkan vitamin Q minimal 1,5 gram dan maksimal 3,5 gram. Banyaknya suplemen A dan B maksimal yang harus dikonsumsi setiap bulannya adalah ... gram.
40
35
30
25
15
Iklan
S. Nur
Master Teacher
24
0.0 (0 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia