Diketahui suatu sistem pertidaksamaan 2x+y≤10;x+y≤6;x+2y≤10;x≥0; dan y≥0. Tentukan luas daerah himpunan penyelesaiannya.

Pertanyaan

Diketahui suatu sistem pertidaksamaan $2x+y\leq10;x+y\leq6;x+2y\leq10;x\geq0;\;\mathrm{dan}\;y\geq0$ . Tentukan luas daerah himpunan penyelesaiannya.

A. Askariawati

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Pembahasan

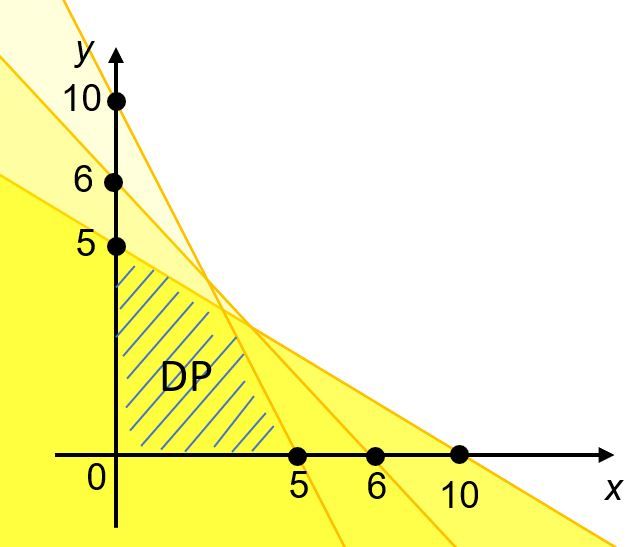
Menentukan himpunan penyelesaian dari sistem pertidaksamaan linear dua variabel (SPtLDV) artinya mencari daerah hasil penyelesaian (DHP) tiap-tiap pertidaksamaan. Kemudian irisan dari DHP tiap pertidaksamaan merupakan DHP dari SPtLDV tersebut. Sebelumnya, daerah penyelesaian dalam pembahasan ini, adalah daerah yang berwarna.

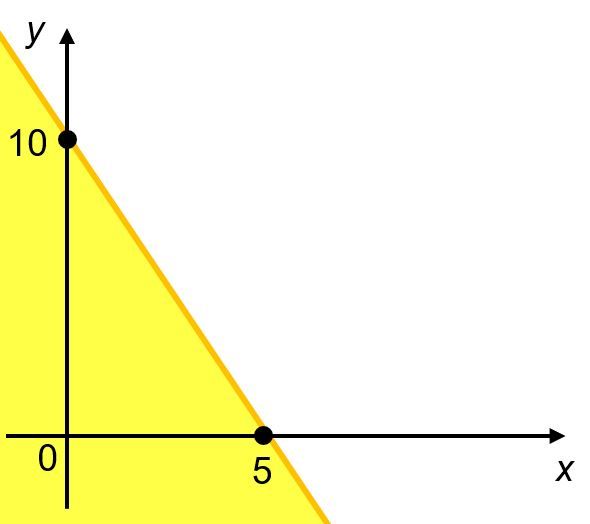
Pertidaksamaan $2x+y\leq10$

Jika $x=0$ maka $y=10\Rightarrow(0,10)$
Jika $y=0$ maka $x=5\Rightarrow(5,0)$

Kemudian, hubungkan titik $(0,10)\;\mathrm{dan}\;(5,0)$ , karena $\leq$ maka garisnya penuh (tidak putus-putus). Ujilah salah satu titik, untuk menentukan daerah penyelesaiannya, misalkan uji titik $(0,0)$ . Dengan mensubstitusi $(0,0)$ ke dalam pertidaksamaan, didapatkan bahwa,

$\begin{array}{rcl}2x+y&=&{2(0)+0}\\&=&0\end{array}$

Dengan membandingkan nilai yang diperoleh dengan nilai yang berada di ruas kanan pertidaksamaan, didapatkan bahwa $0\leq10$ , akibatnya titik $(0,0)$ merupakan titik yang berada dalam daerah penyelesaian $2x+y\leq10$ . Sehingga arsir daerahnya, seperti gambar berikut:

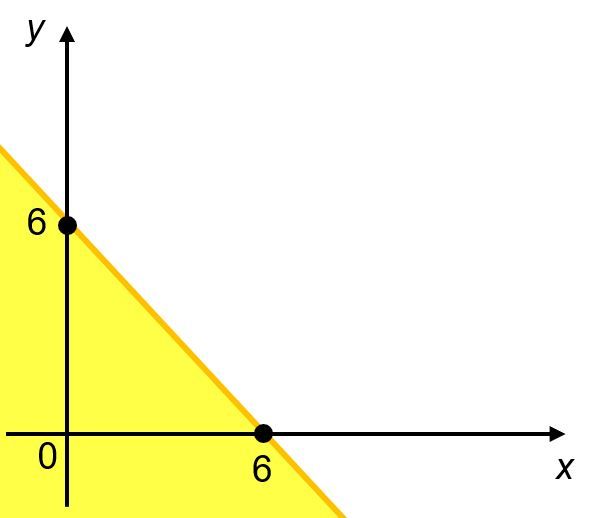
Pertidaksamaan $x+y\leq6$

Jika $x=0$ maka $y=6\Rightarrow(0,6)$
Jika $y=0$ maka $x=6\Rightarrow(6,0)$

Kemudian, hubungkan titik $(0,6)\;\mathrm{dan}\;(6,0)$ , karena $\leq$ maka garisnya penuh (tidak putus-putus). Ujilah salah satu titik, untuk menentukan daerah penyelesaiannya, misalkan uji titik $(0,0)$ . Dengan mensubstitusi $(0,0)$ ke dalam pertidaksamaan, didapatkan bahwa,

$\begin{array}{rcl}x+y&=&{0+0}\\&=&0\end{array}$

Dengan membandingkan nilai yang diperoleh dengan nilai yang berada di ruas kanan pertidaksamaan, didapatkan bahwa $0\leq6$ , akibatnya titik $(0,0)$ merupakan titik yang berada dalam daerah penyelesaian $x+y\leq6$ . Sehingga arsir daerahnya, seperti gambar berikut:

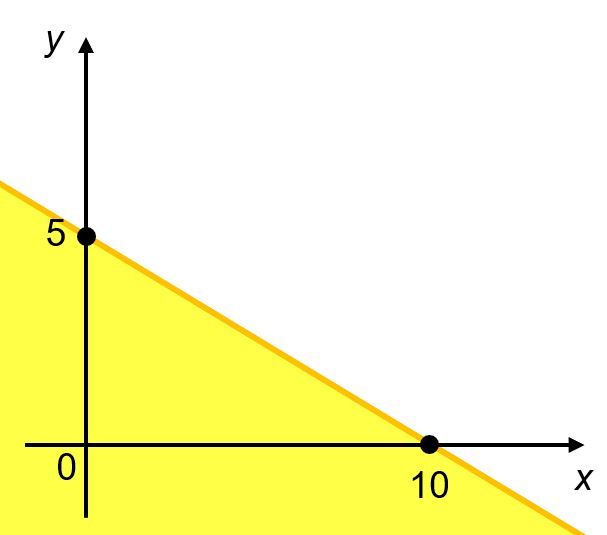
Pertidaksamaan $x+2y\leq10$

Jika $x=0$ maka $y=5\Rightarrow(0,5)$
Jika $y=0$ maka $x=10\Rightarrow(10,0)$

Kemudian, hubungkan titik $(0,5)\;\mathrm{dan}\;(10,0)$ , karena $\leq$ maka garisnya penuh (tidak putus-putus). Ujilah salah satu titik, untuk menentukan daerah penyelesaiannya, misalkan uji titik $(0,0)$ . Dengan mensubstitusi $(0,0)$ ke dalam pertidaksamaan, didapatkan bahwa,

$\begin{array}{rcl}x+2y&=&0+{2(0)}\\&=&0\end{array}$

Dengan membandingkan nilai yang diperoleh dengan nilai yang berada di ruas kanan pertidaksamaan, didapatkan bahwa $0\leq10$ , akibatnya titik $(0,0)$ merupakan titik yang berada dalam daerah penyelesaian $x+2y\leq10$ . Sehingga arsir daerahnya, seperti gambar berikut:

Pertidaksamaan $x\geq0$

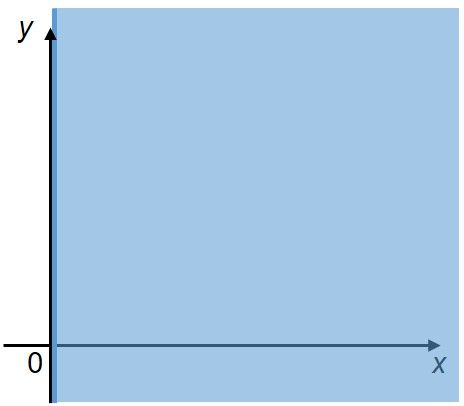
Dan pertidaksamaan $y\geq0$

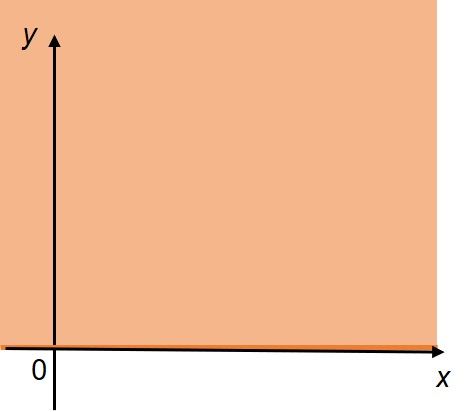
Dengan demikian, diperoleh bahwa penyelesaian dari SPtLDV tersebut adalah irisan dari DHP kelima pertidaksamaan, yaitu

128

0.0 (0 rating)

Pertanyaan serupa

Di antara pilihan jawaban berikut ini, yang menggambarkan daerah penyelesaian dari x−2y≥−2, x+y≤4, x≥0, y≥0 adalah ....

246

0.0

Jawaban terverifikasi

Diketahui suatu sistem pertidaksamaan ⎩⎨⎧−3x+2y≤6x+2y≥−2x≤2y≤3 a. Gambarkan daerah penyelesaiannya pada bidang koordinat kartesius. b. Tentukan luas daerah penyelesaiannya.

563

5.0

Jawaban terverifikasi

Gambarlah himpunan penyelesaian dari sistem-sistem pertidaksamaan berikut! a. x≥0;y≥0;5x+3y≥15

0.0

Jawaban terverifikasi

Sistem pertidaksamaan pada gambar di bawah ini adalah ....

5.0

Jawaban terverifikasi

Daerah yang diarsir pada gambar di bawah ini merupakan penyelesaian dari pertidaksamaan ….

0.0

Jawaban terverifikasi