Diketahui sistem persamaan: x − 2 y + z 3 x + y − 2 z 7 x − 6 y − z ​ = = = ​ 6 4 10 ​ Maka nilai x − y + z = .... dan buatgrafik.

Pembahasan

Sistem persamaan linear tiga variabel (SPLTV) di atas, dapat diselesaikan dengan menggunakan metode eliminasi-substitusi. Eliminasi variabel z dari persamaan pertama dan persamaan kedua pada SPLTV: x − 2 y + z = 6 3 x + y − 2 z = 4 ​ ∣ × 2∣ ∣ × 1∣ ​ 2 x − 4 y + 2 z = 12 3 x + y − 2 z = 4 5 x − 3 y = 16 ​ + ​ ​ Eliminasi variabel z dari persamaan pertama dan persamaan ketiga pada SPLTV: x − 2 y + z = 6 7 x − 6 y − z = 10 8 x − 8 y = 16 ​ + ​ ​ Eliminasi variabel y dari persamaan 5 x − 3 y = 16 dan persamaan 8 x − 8 y = 16 : 5 x − 3 y = 16 8 x − 8 y = 16 ​ ∣ × 8∣ ∣ × 3∣ ​ 40 x − 24 y = 128 24 x − 24 y = 48 16 x = 80 x = 16 80 ​ = 5 ​ − ​ ​ Substitusi x = 5 ke persamaan 8 x − 8 y = 16 : 8 x − 8 y 8 ( 5 ) − 8 y 40 − 8 y − 8 y − 8 y y ​ = = = = = = = ​ 16 16 16 16 − 40 − 24 − 8 − 24 ​ 3 ​ Substitusi x = 5 dan y = 3 ke persamaan x − 2 y + z = 6 : x − 2 y + z ( 5 ) − 2 ( 3 ) + z 5 − 6 + z − 1 + z z ​ = = = = = = ​ 6 6 6 6 6 + 1 7 ​ Sehingga nilai x − y + z , yaitu: x − y + z ​ = = ​ 5 − 3 + 7 9 ​ Grafik dari sistem persamaan linear tiga variabel dapat dibuat dengan menggambar setiap persamaan linear. Titik potong ketiga persamaan linear tiga variabel tersebut, yaitu: x = 5 , y = 3 , dan z = 7 . Titik potong persamaan x − 2 y + z = 6 terhadap sumbu- x , sumbu- y , dan sumbu- z berturut-turut adalah ( 6 , 0 , 0 ) , ( 0 , − 3 , 0 ) dan ( 0 , 0 , 6 ) . Titik potong persamaan 3 x + y − 2 z = 4 terhadap sumbu- x , sumbu- y , dan sumbu- z berturut-turut adalah ( 3 4 ​ , 0 , 0 ) , ( 0 , 4 , 0 ) dan ( 0 , 0 , − 2 ) . Titik potong persamaan 7 x − 6 y − z = 10 terhadap sumbu- x , sumbu- y , dan sumbu- z berturut-turut adalah ( 7 10 ​ , 0 , 0 ) , ( 0 , − 3 5 ​ , 0 ) dan ( 0 , 0 , − 10 ) . 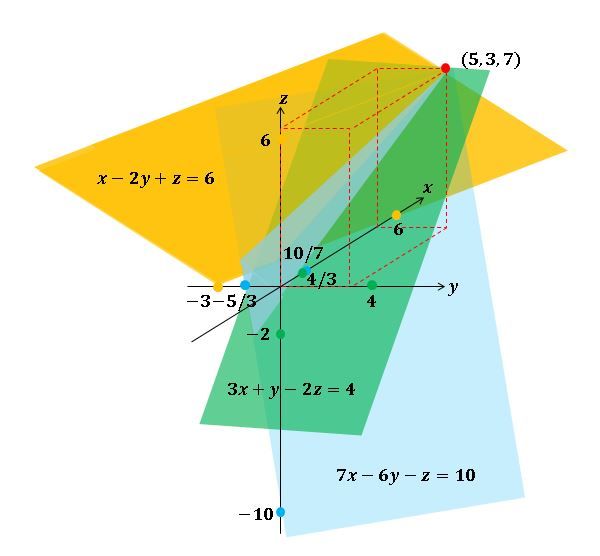Berikut adalah grafik dari sistem persamaan linear tiga variabel tersebut: Dengan demikian, nilai x − y + z = 9 dan grafik di atas adalah grafik sistem persamaan linear tersebut.