Diketahui sebuah kubus ABCD.EFGH dengan panjang rusuk 12 cm. Jarak antara titik B ke bidang DEG adalah … cm.

Pembahasan

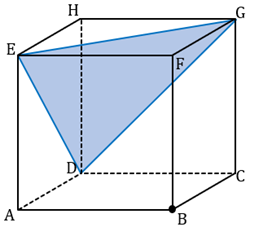
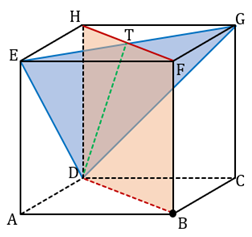
Perhatikan gambar di bawah ini : Perhatikan bidang BDHF sebagai berikut Perhatikan bahwa HF tegak lurus EG karena keduanya adalah diagonal sisi pada suatu sisi kubus. Sehingga HF dan EG tegak lurus. Selanjutnya, BF tegak lurus EFGH. Sehingga BF tegak lurus dengan seluruh garis pada bidang EFGH, salah satunya adalah EG. Maka BF tegak lurus dengan EG. Karena HF tegak lurus dengan EG dan BF tegak lurus dengan EG, maka BDHF tegak lurus dengan EG. Maka BDHF tegak lurus dengan seluruh bidang yang memuat maupun sejajar dengan EG, salah satunya DEG. Maka BDHF tegak lurus dengan DEG dan berpotongan pada garis DT. Karena B terletak di bidang BDHF, maka jarak dari B ke bidang DEG sama saja dengan jarak dari B ke garis DT. Sehingga perhatikan segitiga BDT. 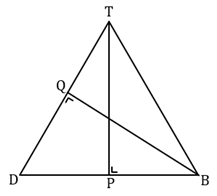Garis TP dan BQ adalah garis tinggi pada segitiga BDT. Karena BQ adalah garis tinggi pada segitiga BDT, maka jarak dari B ke DT sama saja dengan panjang ruas garis BQ. Cari panjang sisi dari masing-masing sisi segitiga BDT. Perhatikan bahwa dengan panjang rusuk kubus 12 cm, maka didapat dan . Perhatikan TP = AE = 12 cm. Sehingga dengan menggunakan perbandingan luas segitiga BDT, didapat bahwa cm.