Diketahui kubus ABCD.EFGH dengan panjang rusuk 2 2 ​ cm . Jika titik P berada di tengah-tengah AB dan titik Q berada di tengah-tengah BC, maka jarak antara titik H dengan garis PQ adalah ... cm . (SBMPTN 2018)

Pembahasan

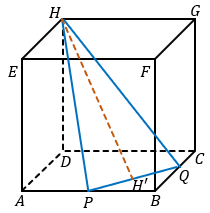
Diketahui kubus ABCD.EFGH dengan panjang rusuk ,titik Pdi tengah-tengah AB, dan titik Q di tengah-tengah BC. Perhatikan gambar berikut! Misal adalah jarak titik H dengan garis PQ. Perhatikan bahwa merupakan setelah panjang rusuk kubus, maka panjang adalah . Kemudian, perhatikan juga bahwa juga setengah panjang rusuk kubus sehinggapanjang adalah . Dengan menggunakan Teorema Pythagoras, makadiperoleh persamaan sebagai berikut. Karena merupakan suatu sisi, maka tidak mungkin bernilai negatif. Jadi, panjang . Untuk menentukan panjang HP, tarikgaris dari titik Hke titik Akemudian hubungkan dengan garis AP, sehingga terbentuklah segitiga AHPsiku-siku di titik A. Perhatikan bahwa AHmerupakan diagonal sisi kubus, maka panjang AHadalah . Lalu, APmerupakan setelah panjang rusuk sehinggapanjang APadalah . Dengan menggunakan Teorema Pythagoras, makadiperoleh sebagai berikut. Karena HPmerupakan suatu sisi, maka tidak mungkin bernilai negatif. Jadi, panjang . Selanjutnya, untuk menentukan panjang HQ,tarikgaris dari titik Hke titik Ckemudian hubungkan dengan garis CQsehingga terbentuklah segitiga CHQsiku-siku di titik C. Perhatikan bahwa CH merupakandiagonal sisi kubus. Dengan menggunakan cara yang sama dengan menentukanpanjang AH,maka diperoleh . Kemudian, CQmerupakan setelah panjang rusuk. Denganmenggunakan cara yang sama dengan menentukanpanjang AP,maka diperoleh . Dengan demikian, panjang HQsama dengan panjang HPyaitu . Karena , maka segitiga PHQadalah segitiga sama kaki seperti gambar di bawah ini. 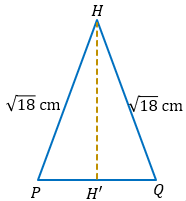Jadi,dengan menggunakan teorema Pythagorasjarak titik H dengan garis PQ adalah sebagai berikut. Karena panjang HH' tidak mungkin bernilai negatif, maka diambil . Dengan demikian, jawaban yang tepat adalah C.