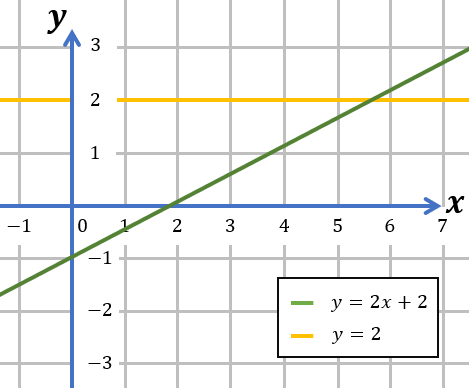Diberikanfungsi f : R → R dengan f ( x ) = x + 5 dan g : R → R dengan g ( x ) = x − 3 . Fungsi di bawah ini yang merupakan fungsi bijektif adalah ....

Pembahasan

Sebelumnya, ingat kembali bahwa sebuah fungsi disebutbijektif jika fungsi adalah fungsisurjektif dan injektif. Dari soal, diberikan fungsi dengan dan dengan . Akan dicari fungsi yang merupakan fungsi bijektif. Untuk mengerjakan soal, akan diperiksa masing-masing pilihan jawaban. Perhatikan bahwa pada opsi A, didapat yang merupakan fungsi linear. Untuk mencari tahu apakah adalah fungsi injektifatau bukan, digunakan garis horizontal sebagai berikut. 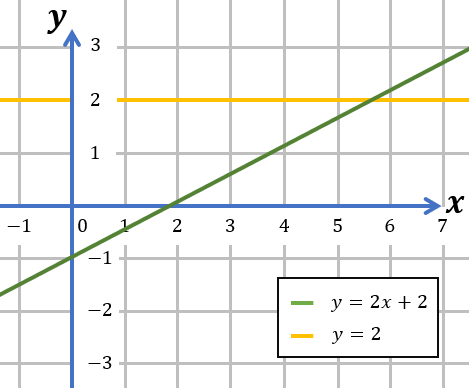Perhatikan bahwa fungsi linear memetakan seluruh anggota domain ke anggota kodomain Perhatikan bahwa, karena adalah kurva linear, maka garis horizontal hanya akan memotong kurva di satu titik. Artinya, untuk nilai hanya dipasangkan kenilai yang berbeda, sehingga . Maka adalah fungsi injektif . Dan juga, perhatikan bahwa karena kurva berbentuk garis lurus yang terus merentang, maka setiap anggota kodomain pada sumbu tegak pasti akan terpetakan oleh . Artinya, range dari fungsi ini adalah kodomain. Sehingga, adalah fungsi surjektif . Karena adalah fungsi surjektif dan injektif, maka adalah bijektif . Opsi A tepat . Kemudian, perhatikan bahwa pada opsi B didapat yang merupakan fungsi konstan. Artinya, setiap nilai hanya akan dipetakan ke satu nilai, yaitu . Maka, range dari fungsi ini adalah , bukan seluruh bilangan real. Sehingga fungsi ini bukan fungsi surjektif. Untuk lebih jelasnya, perhatikan gambar berikut ini! 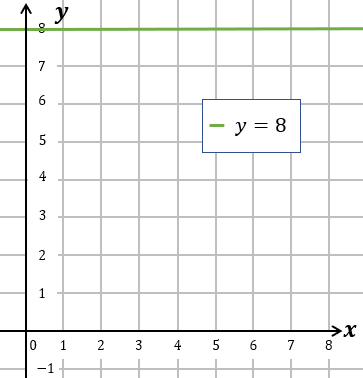Perhatikan bahwa terdapat anggota kodomain, misalkan , tidak memiliki pasangan. Artinya, fungsi ini juga bukan fungsi bijektif. Opsi B tidak tepat. Selanjutnya, perhatikan pada opsi C didapat yang merupakan fungsi kuadrat. Artinya, bentuk kurvanya adalah sebuahparabola yang memiliki titik maksimum atau minimum. Hal ini mengakibatkanadanyaanggota pada kodomain yang berada di bawah titik minimum atau di atas titik maksimum yang tidak terpetakan ke salah satu anggota pada domainnya. Sehingga ada anggota kodomain yang tidak termasuk dalam range. Maka fungsi ini tidak bersifat surjektif. Untuk lebih jelasnya, perhatikan gambar berikut ini! Perhatikan bahwa terdapat anggota kodomain, misalkan , tidak memiliki pasangan. Artinya, fungsi ini juga tidakbijektif. Opsi C tidak tepat. Kemudian, pehatikan bahwa pada opsi D didapat yang juga merupakan fungsi kuadrat.Artinya, bentuk kurvanya adalah sebuahparabola yang memiliki titik maksimum atau minimum. Hal ini mengakibatkanadanyaanggota pada kodomain yang berada di bawah titik minimum atau di atas titik maksimum yang tidak terpetakan ke salah satu anggota pada domainnya. Sehingga ada anggota kodomain yang tidak termasuk dalam range. Maka fungsi ini tidak bersifat surjektif. Untuk lebih jelasnya, perhatikan gambar berikut ini! Perhatikan bahwa terdapat anggota kodomain, misalkan , tidak memiliki pasangan. Artinya, fungsi ini juga tidakbijektif. Opsi Dtidak tepat. Selanjutnya, perhatikan bahwa pada opsi E didapat yang merupakan fungsi konstan.Artinya, setiap nilai hanya akan dipetakan ke satu nilai, yaitu . Maka, range dari fungsi ini adalah , bukan seluruh bilangan real. Sehingga fungsi ini bukan fungsi surjektif. Untuk lebih jelasnya, perhatikan gambar berikut ini! Perhatikan bahwa terdapat anggota kodomain, misalkan , tidak memiliki pasangan. Artinya, fungsi ini juga bukan fungsi bijektif. Opsi E tidak tepat. Jadi, jawabannya adalah A.