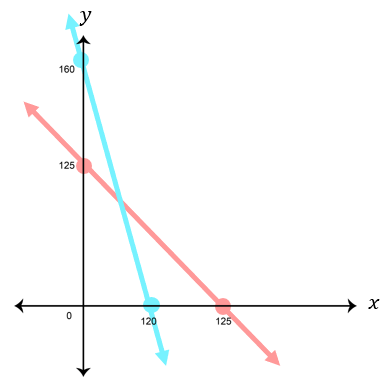
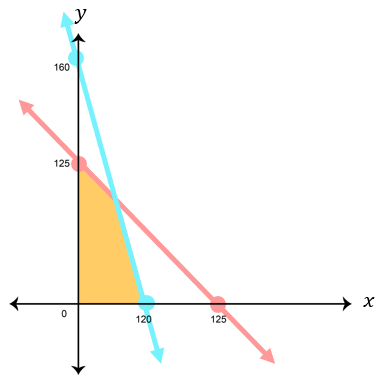
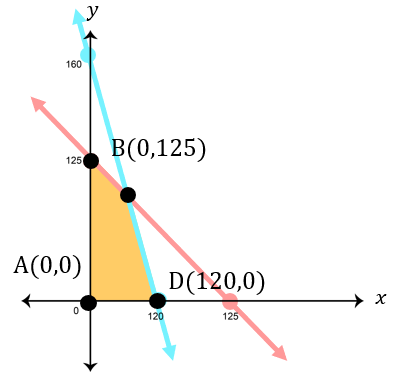
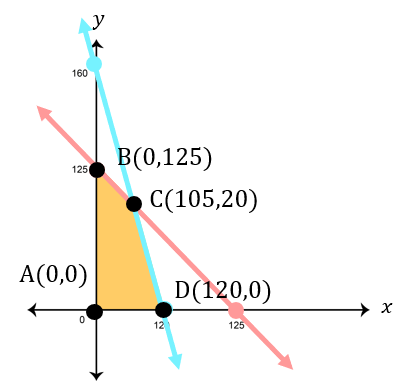
Di atas tanah seluas 1 , 2 hektar akan dibangun dua tipe rumah, yaitu tipe A dan tipe B. Tiap unit rumah tipe A luasnya 100 m 2 , sedangkan tipe B luasnya 75 m 2 . Jumlah rumah yang akan dibangun paling banyak 125 unit . Harga jual rumah tipe A adalah Rp100.000.000,00 dan rumah tipe A adalah Rp60.000.000. Tentukan : b. pendapatan maksimum hasil penjualan seluruh rumah.

Pembahasan

Misalkan: x : jumlah rumah tipe A y : jumlah rumah tipe B Maka soal tersebut dalam dibuat menjadi model matematika sebagai berikut. Selanjutnya gambarkan daerah himpunan penyelesaian dari sistem pertidaksamaan tersebut. Pertama tentukan titik potong sumbu koordinat setiap garis (anggap pertidaksamaan menjadi suatu persamaan): Maka, menghasilkan titik dan serta menghasilkan titik dan . Dari titik tersebut dibuat garis dan digambar pada bidang kartesius sebagai berikut. Persamaan x + y = 125 diwakilkan dengan garis berwarna merah muda sedangkan garis 4 x + 3 y = 480 diwakilkan dengan garis berwarna biru. Selanjutnya uji titik untuk menentukan daerah penyelesaian(bebas baik di atas maupun di bawah garis). Titik tersebut di substitusikan ke sistem pertidaksamaan di awal. Jika pernyataannya menjadi benar maka titik tersebut termasuk dalampenyelesaiannya. Daerah penyelesaian merupakan daerah irisan yang diperoleh dari masing-masing penyelesaian pertidaksamaan tersebut. Untuk mengetahui nilai maksimum, kita cari titik pojok terlebih dahulu. Ternyata ada salah satu titik pojok yang belum diketahui lokasinya. Karena merupakan perpotongan dua buah garis yang persamaannya sudah kita temukan sebelumnuya, maka untuk mencari titik tersebut kita bisa lakukan dengan metode eliminasi-substitusi kedua persamaan itu. Kemudian substitusikan nilai x ke salah satu persamaan tersebut untuk mendapat nilai y . x + y 105 + y y ​ = = = ​ 125 125 20 ​ Sehingga titik potong dua garis adalah . Selanjutnya substitusi titik pojok ke fungsi objektif untuk memperoleh nilai maksimum : A ( 0 , 0 ) B ( 0 , 125 ) C ( 105 , 20 ) D ( 120 , 0 ) ​ → = = → = = → = = → = = ​ f ( 0 , 0 ) = 100.000.000 ( 0 ) + 60.000.000 ( 0 ) 0 + 0 0 f ( 0 , 125 ) = 100.000.000 ( 0 ) + 60.000.000 ( 125 ) 0 + 7.500.000.000 7.500.000.000 f ( 105 , 20 ) = 100.000.000 ( 105 ) + 60.000.000 ( 20 ) 10.500.000.000 + 1.200.000.000 11.700.000.000 f ( 120 , 0 ) = 100.000.000 ( 120 ) + 60.000.000 ( 0 ) 12.000.000.000 12 . 000 . 000 . 000 ​ Dengan demikian, pendapatan hasil penjualan seluruh rumah adalah Rp12.000.000.000 dengan penjualan tipe A sebanyak 120 unit dan tipe B 0 unit.