Daerah penyelesaian merupakan daerah tertutup yang dibatasi oleh empat pertidaksamaan. Langkah pertama adalah kita ketahui terlebih dahulu garis-garis yang membatasinya seperti berikut:
- Garis yang melalui titik (2, 0) dan (1, 3).
Dengan menggunakan rumus persamaan garis yang melalui dua titik koordinat, maka:
3−0y−03y−y−y3x+y=====1−2x−2−1x−23(x−2)3x−66
- Garis yang melalui (1, 3) dan (3, 5).
Dengan menggunakan rumus persamaan garis yang melalui dua titik koordinat, maka:
5−3y−3=3−1x−12y−3=2x−1y−3=x−1x−y=−3+1x−y=−2
- Garis yang melalui (3, 5) dan (4, 0).
Dengan menggunakan rumus persamaan garis yang melalui dua titik koordinat, maka:
0−5y−5−5y−5y−5y−55x+y5x+y======4−3x−31x−3−5(x−3)−5x+1515+520
y=0
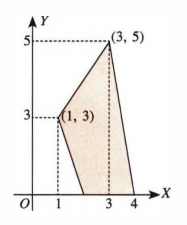
Garis yang telah kita buat di atas kita uraikan dalam gambar sebagai berikut:

Untuk menentukan SPLtdVnya, kita gunakan uji titik untuk masing- masing garis seperti berikut:
- SPLtdV yang berhubungan dengan garis 3x+y=6.
Daerah diarsir terletak di atas garis 3x+y=6, terdapat titik (3, 0) pada daerah tersebut, sehingga dengan mengunakan uji titik, maka:
3(3)+09≥≥66
Agar bentuknya benar maka tanda pertidaksamaan haruslah ≥, sehingga daerah arsir diabatasi oleh salah satu SPLtdV yaitu 3x+y≥6.
- SPLtdV yang berhubungan dengan garis x−y=−2.
Daerah diarsir terletak di bawah garis x−y=−2, terdapat titik (3, 0) pada daerah tersebut, sehingga dengan mengunakan uji titik, maka:
3−03≥≥−2−2
Agar bentuknya benar maka tanda pertidaksamaan haruslah ≥, sehingga daerah arsir diabatasi oleh salah satu SPLtdV yaitu x−y≥−2.
- SPLtdV yang berhubungan dengan garis 5x+y=20.
Daerah diarsir terletak di bawah garis 5x+y=20, terdapat titik (3, 0) pada daerah tersebut, sehingga dengan mengunakan uji titik, maka:
5(0)+00≤≤2020
Agar bentuknya benar maka tanda pertidaksamaan haruslah ≤, sehingga daerah arsir diabatasi oleh salah satu SPLtdV yaitu 5x+y≤20..
- SPLtdV yang berhubungan dengan garis y=0.
Karena daerah arsir berada di atas garis y=0, maka tanda pertidaksamaan adalah ≥, sehingga SPLtdV nya adalah y≥0.
Sehingga, daerah penyelesaian pada soal dibatasi oleh empat pertidaksamaan di atas yang terdiri dari:
 ,
,  ,
,  ,
, 
Oleh karena itu, jawaban yang tepat adalah A.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,














