Untuk menentukan himpunan penyelesaian dari sistem pertidaksamaan x+y≤5, 5x−2y≤10, y−x≤2, x≥0 dan y≥0, kita cari penyelesaian dari masing-masing ketiga pertidaksamaan tersebut, kemudian kita iriskan ketiga seperti berikut:
- Himpunan penyelesaian x+y≤5.
Untuk menentukan himpununan x+y≤5 kita gambar terlebih dahulu garis x+y=5 sebagai berikut:
1. Titik potong sumbu x, y=0.
x+yx+0x===555
Sehingga titik potong sumbu x garis x+y=5 adalah (5, 0).
2. Titik potong sumbu y, x=0.
x+y0+yy===555
Sehingga titik potong sumbu y garis 4x+y=8 adalah (0, 5).
Jadi, gambar garis x+y=5 adalah garis yang melalui titik (5, 0) dan (0, 5) seperti gambar berikut:

Untuk menentukan himpunan penyelesaian dari x+y≤5 kita dapat menggunakan uji titik. Misalkan titik yang kita uji adalah titik di bawah garis yaitu (0, 0), maka:
x+y0+00≤≤≤555
Karena menghasilkan bentuk yang benar, maka daerah penyelesaian adalah daerah yang bawah, sehingga penyelesaian dari x+y≤5 adalah:

- Himpunan penyelesaian 5x−2y≤10.
Untuk menentukan himpununan 5x−2y≤10 kita gambar terlebih dahulu garis 5x−2y=10 sebagai berikut:
1. Titik potong sumbu x, y=0.
5x−2y5x−2(0)5xx====1010102
Sehingga titik potong sumbu x garis 5x−2y=10 adalah (2, 0).
2. Titik potong sumbu y, x=0
5(0)−2y−2yy===1010−5
Sehingga titik potong sumbu y garis 5x−2y=10 adalah (0, −5).
Jadi, gambar garis 5x−2y=10 adalah garis yang melalui titik (2, 0) dan (0, −5) seperti gambar berikut:

Untuk menentukan himpunan penyelesaian dari 5x−2y≤10 kita dapat menggunakan uji titik. Misalkan titik yang kita uji adalah titik di atas garis yaitu (0, 0), maka:
5x−2y5(0)−2(0)0≤≤≤101010
Karena menghasilkan bentuk yang benar, maka daerah penyelesaian adalah daerah yang atas, sehingga penyelesaian dari 3x+4y≤24 adalah:

- Himpunan penyelesaian y−x≤2.
Untuk menentukan himpununan y−x≤2 kita gambar terlebih dahulu garis y−x=2 sebagai berikut:
1. Titik potong sumbu x, y=0.
0−xx==2−2
Sehingga titik potong sumbu x garis y−x=2 adalah (−2, 0).
2. Titik potong sumbu y, x=0.
y−0y==22
Sehingga titik potong sumbu y garis y−x=2 adalah (0, 2).
Jadi, gambar garis y−x=2 adalah garis yang melalui titik (−2, 0) dan (0, 2) seperti gambar berikut:

Untuk menentukan himpunan penyelesaian dari y−x≤2 kita dapat menggunakan uji titik. Misalkan titik yang kita uji adalah titik di bawah garis yaitu (0, 0), maka:
y−x0−00≤≤≤222
Karena menghasilkan bentuk yang benar, maka daerah penyelesaian adalah daerah yang bawah, sehingga penyelesaian dari y−x≤2 adalah:

- Himpunan penyelesaian dari x≥0
Himpunan penyelesaian dari x≥0 adalah daerah di kanan dari garis x=0 atau sumbu y.

- Himpunan penyelesaian dari y≥0.
Himpunan penyelesaian dari y≥0 adalah daerah di atas dari garis x=0 atau sumbu y.

- Himpunan penyelesaian dari x+y≤5, 5x−2y≤10, y−x≤2, x≥0, dan y≥0.
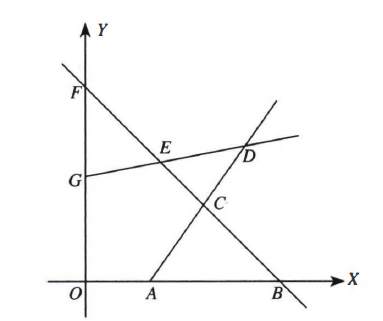
Kita iriskan himpunan penyelesaian dari ketiga pertidaksamaan x+y≤5, 5x−2y≤10, y−x≤2, x≥0, dan y≥0 sehingga menjadi daerah seperti berikut:

Pada soal, daerah yang diarsir disebut daerah OACEG.
Oleh karena itu, jawaban yang tepat adalah E.