Daerah yang diarsir pada gambar di bawah ini merupakan himpunan penyelesaian dari....

Pembahasan

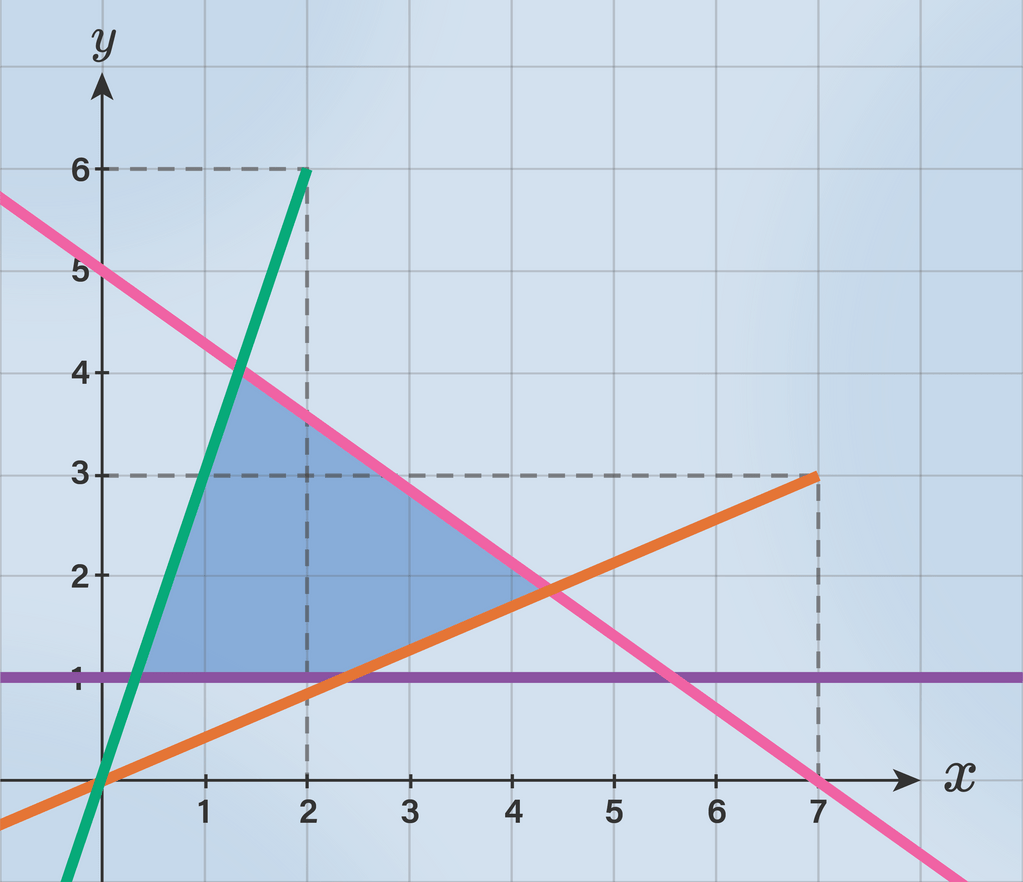
Ingat bahwa: Persamaan garis lurus melalui titik ( x 1 ​ , y 1 ​ ) dan ( x 2 ​ , y 2 ​ ) adalah y 2 ​ − y 1 ​ y − y 1 ​ ​ = x 2 ​ − x 1 ​ x − x 1 ​ ​ . 1. Tentukan persamaan masing-masing garis. Perhatikan garis berwarna pink. Garis melalui titik ( 0 , 5 ) dan ( 7 , 0 ) , maka persamaannya adalah: y 2 ​ − y 1 ​ y − y 1 ​ ​ 0 − 5 y − 5 ​ − 5 y − 5 ​ 7 y − 35 7 y + 5 x ​ = = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 7 − 0 x − 0 ​ 7 x ​ − 5 x 35 ​ Perhatikan garis berwarna hijau. Garis melalui titik ( 0 , 0 ) dan ( 2 , 6 ) , maka persamaannya adalah: y 2 ​ − y 1 ​ y − y 1 ​ ​ 6 − 0 y − 0 ​ 6 y ​ 2 y y ​ = = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 2 − 0 x − 0 ​ 2 x ​ 6 x 3 x ​ Perhatikan garis berwarna oranye. Garis melalui titik ( 0 , 0 ) dan ( 7 , 3 ) , maka persamaannya adalah: y 2 ​ − y 1 ​ y − y 1 ​ ​ 3 − 0 y − 0 ​ 3 y ​ 7 y ​ = = = = ​ x 2 ​ − x 1 ​ x − x 1 ​ ​ 7 − 0 x − 0 ​ 7 x ​ 3 x ​ Perhatikan garis berwarna ungu. Garis berwarna ungu persamaannya adalah y = 1 . 2. Tentukan pertidaksamaan menggunakan titik uji. (Misal ambil titik uji ( 2 , 3 ) ). 5 x + 7 y = 35 5 x + 7 y ​ = = ​ 5 ⋅ 2 + 7 ⋅ 3 31 ​ Karena 31 ≤ 35 dan titik ( 2 , 3 ) berada dalam daerah penyelesaian, maka pertidaksamaannya menjadi 5 x + 7 y ​ ≤ ​ 35 ​ . y = 3 x Ketika disubstitusikan x = 2 dan y = 3 akan diperoleh 3 ≤ 6 , sehingga pertidaksamaannya menjadi y ≤ 3 x . 7 y = 3 x Ketika disubstitusikan x = 2 dan y = 3 akan diperoleh 21 ≥ 6 , sehingga pertidaksamaannya menjadi 7 y ≥ 3 x atau 3 x ≤ 7 y y = 1 y = 1 , daerah yang diarsir di sebelah atasnya, maka pertidaksamaannya adalah: y ≥ 1 . Jadi, persamaan garisnya adalah 5 x + 7 y ≤ 35 ; y ≤ 3 x ; 3 x ≤ 7 y ; y ≥ 1 Oleh karena itu, jawaban yang benar adalah C.