Gambar berikut yang menunjukkan daerah himpunan penyelesaian (daerah yang diarsir) untuk sistem pertidaksamaan: { x + y + x y + 10 ≤ 0 x 2 + y 2 − 100 ≤ 0 ​ adalah ....

Pembahasan

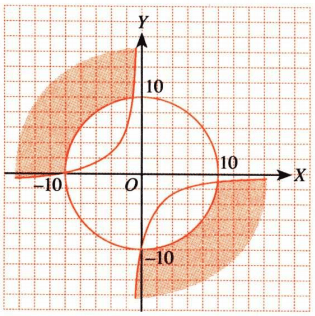
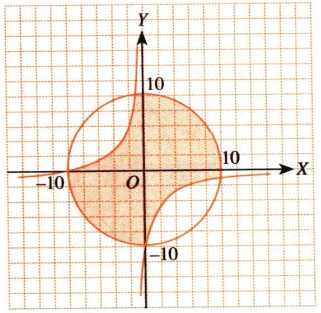
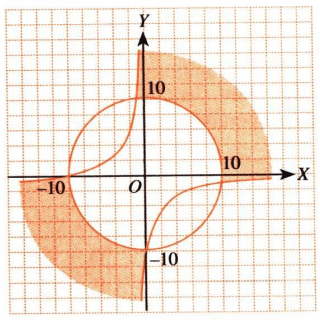
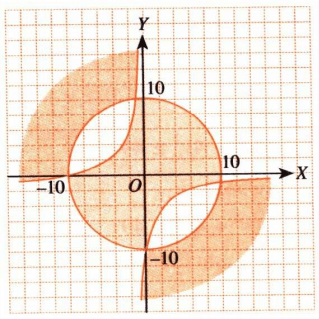
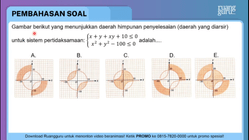
Gunakan cara menentukan daerah penyelesaian sistem pertidaksamaan kuadrat dua variabel dengan mengecek salah satu titik ke pertidaksamaan tersebut. Sebelumnya, identifikasi pertidaksamaan terlebih dahulu x 2 + y 2 − 100 ≤ 0 Ubah pertidaksamaan x 2 + y 2 − 100 ≤ 0 menjadi sebuah persamaan x 2 + y 2 − 100 = 0 untuk menentukan gambar pada diagram kartesius. x 2 + y 2 − 100 x 2 + y 2 x 2 + y 2 ​ = = = ​ 0 100 1 0 2 ​ x 2 + y 2 = 1 0 2 merupakan persamaan lingkaran dengan pusat ( 0 , 0 ) dan r = 0 . Sehingga x + y + x y + 10 = 0 merupakan kurva lengkungnya. 2. Tentukan darah penyelesaian mnggunakan titik uji. Akan ditentukan daerah himpunan penyelesaian (daerah yang diarsir) untuk sistem pertidaksamaan: . Karena gambar kurva pada pilihan ganda semuanya sama, maka agar lebih mudah dengan menentukan daerah penyelesaiannya saja dengan memilih titik pusat atau kemudian substitusikan pada pertidaksamaan tersebut. *Menentukan daerah penyelesaian dari yang merupakan kurva yang berbentuk hiperbola. Diperoleh bahwa hasilnya bernilai salah untuk substitusi titik , sehingga daerah penyelesaiannya adalah daerah yang menjauhi titik . *Menentukan daerah penyelesaian dari yang merupakan kurva yang berbentuk lingkaran. Diperoleh bahwa hasilnya bernilai benar untuk substitusi titik , sehingga daerah penyelesaiannya adalah daerah yang mendekati titik . Sehingga jika kedua kurva tersebut digabungkan akan membentuk seperti berikut. 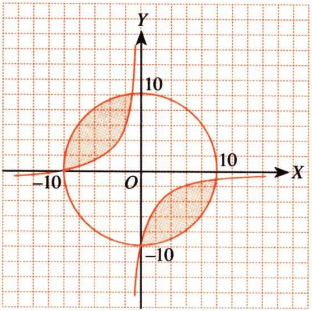Jadi, jawaban yang tepat adalah B.