Iklan
Pertanyaan
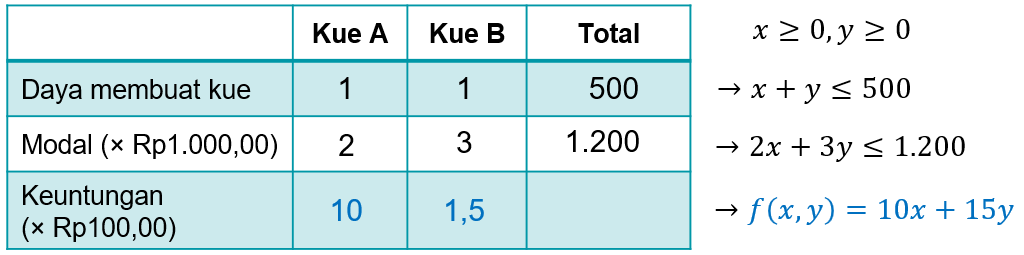
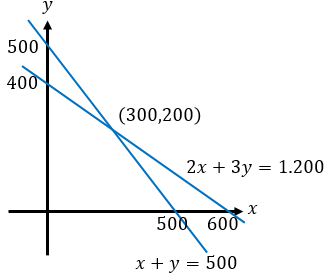
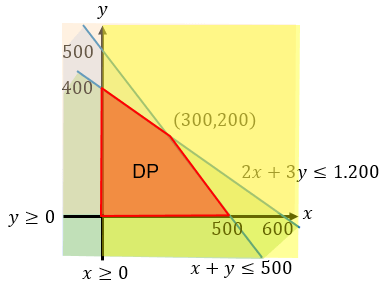
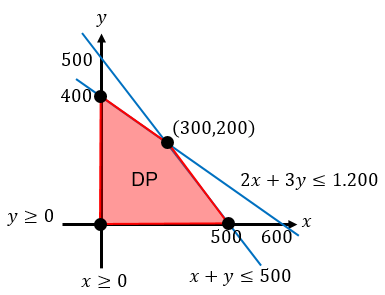
Butet membuat dua jenis kue. Setiap kue A memerlukan modal Rp2.000,00 dan dijual mendapat keuntungan Rp1.000,00 per buah. Sedangkan untuk kue B memerlukan modal Rp3.000,00 dan dijual mendapat keuntungan Rp1.500,00 per buah. Modal yang tersedia Rp1.200.000,00 dan paling banyak hanya dapat membuat 500 kue per hari. Jika kue-kue tersebut terjual habis, keuntungan maksimum yang diperoleh Butet adalah ....
Butet membuat dua jenis kue. Setiap kue A memerlukan modal Rp2.000,00 dan dijual mendapat keuntungan Rp1.000,00 per buah. Sedangkan untuk kue B memerlukan modal Rp3.000,00 dan dijual mendapat keuntungan Rp1.500,00 per buah. Modal yang tersedia Rp1.200.000,00 dan paling banyak hanya dapat membuat 500 kue per hari. Jika kue-kue tersebut terjual habis, keuntungan maksimum yang diperoleh Butet adalah ....
Rp500.000,00
Rp600.000,00
Rp650.000,00
Rp700.000,00
Rp750.000,00
Iklan
S. SMT.Ulfah
Master Teacher
4
5.0 (3 rating)
Shifa Amalia Salsabila
Makasih ❤️
Dewi Maharani
Makasih ❤️
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia