Bila x 2 + x − 2 > 0 maka pertidaksamaan itu dipenuhi oleh ....

Pembahasan

Himpunan penyelesaian dari suatu pertidaksamaan kuadrat, dapat ditentukan dengan menggunakan prosedur berikut ini. Pertama, kita perlu menentukan akar-akar dari harga nol pertidaksamaan kuadrat x 2 + x − 2 > 0 yaitu x 2 + x − 2 = 0 . 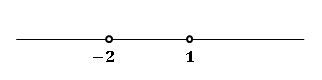Ingat bahwa untuk menentukan akar-akar dari suatu persamaan kuadrat dapat dicari menggunakan cara pemfaktoran sebagai berikut: x 2 + x − 2 ( x − 1 ) ( x + 2 ) x ​ = = = ​ 0 0 1 atau x = − 2 ​ Kemudian dari penyelesaian persamaan kuadrat tersebut, gambar garis bilangan dengan batas x = 1 dan x = − 2 sebagaimana gambar di bawah ini. Dimana batas-batas tersebut tidak termasuk ke dalam daerah penyelesaian (digambar sebagai titik kosong) karena tanda pertidaksamaannya " < ". Selanjutnya akan diselidiki nilai dari masing-masing daerah dengan mengambil satu sampel dari satu daerah. Ambil titik uji x = − 3 , x = 0 , dan x = 2 , kemudian disubstitusikan ke dalam bentuk persamaan kuadratnya. Untuk x = − 3 , nilai persamaan kuadrat menjadi ( − 3 ) 2 + ( − 3 ) − 2 = 4 . Sehingga, daerah yang memuat x = − 3 adalah positif. Untuk x = 0 , nilai persamaan kuadrat menjadi 0 2 + 0 − 2 = − 2 . Sehingga daerah yang memuat x = 0 adalah negatif. Untuk x = 2 , nilai persamaan kuadrat menjadi 2 2 + 2 − 2 = 4 . Sehingga daerah yang memuat x = 2 adalah positif. 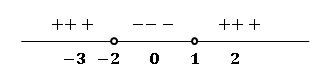Selanjutnya, gambar tanda positif/negatif pada garis bilangan sesuai dengan daerahnya sebagaimana gambarberikut: Karena pertidaksamaan pada soal memiliki tanda" < ", maka himpunan penyelesaiannya ada pada daerah garis bilangan yang memiliki tanda negatif. 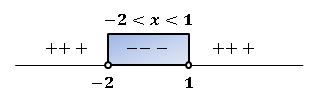Sehingga, himpunan penyelesaiannya yaitu: HP = { x ∣ − 2 < x < 1 , x ∈ R } Dengan demikian, himpunan penyelesaian pertidaksamaan tersebut adalah HP = { x ∣ − 2 < x < 1 , x ∈ R } .