Pertanyaan

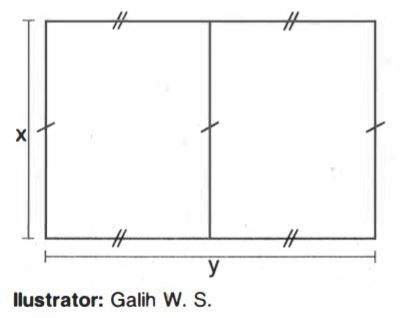
Amir memiliki kawat sepanjang 100 cm . Kawat tersebut akan dibuat dua persegi panjang yang salah satu sisinya berimpit (bersekutu) dengan sisi persegi panjang yang lain seperti gambar berikut. Tentuka nilai x dan y agar luas permukaan kedua persegi panjang maksimum ?

Amir memiliki kawat sepanjang $100 cm$ . Kawat tersebut akan dibuat dua persegi panjang yang salah satu sisinya berimpit (bersekutu) dengan sisi persegi panjang yang lain seperti gambar berikut.

Tentuka nilai $x$ dan $y$ agar luas permukaan kedua persegi panjang maksimum ?

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Pembahasan

Diketahui bahwa terdapat kawat sepanjang 100 cm akan dibuat dua persegi panjang yang salah satu sisinya berimpit (bersekutu) dengan sisi persegi panjang yang lain. Misalkan : panjang persegi panjang dan l : lebar persegi panjang , K : keliling persegi panjang berimpit , L p : luas permukaan persegi panjang berimpitmaka K 100 100 2 y y = = = = = p + p + l + p + p + l 2 1 y + 2 1 y + x + 2 1 y + 2 1 y + x + x 2 y + 3 x 100 − 3 x 2 100 − 3 x Ingat kembali luas permukaan persegi panjang L p = = p ⋅ l y ⋅ x Jika y = 2 100 − 3 x disubstitusikan pada persamaan di atas maka L p = = = y ⋅ x ( 2 100 − 3 x ) ⋅ x 50 x − 2 3 x 2 diperoleh fungsi kuadrat dengan a = − 2 3 dan b = 50 sehingga x mak s = = = − 2 a b − 2 ( − 2 3 ) 50 3 50 diperoleh x mak s = 3 50 cm dan y mak s = = = 2 100 − 3 x 2 100 − 3 ( 3 50 ) 25 cm Dengan demikian,nilai x dan y agar luas permukaan kedua persegi panjang maksimum adalah x = 3 50 cm dan y = 25 cm .

Diketahui bahwa terdapat kawat sepanjang $100 cm$ akan dibuat dua persegi panjang yang salah satu sisinya berimpit (bersekutu) dengan sisi persegi panjang yang lain. Misalkan $p$ : panjang persegi panjang dan $l$ : lebar persegi panjang , $K$ : keliling persegi panjang berimpit , $L_{p}$ : luas permukaan persegi panjang berimpit maka

$K 100100 2 y y = = = = = p + p + l + p + p + l \frac{1}{2} y + \frac{1}{2} y + x + \frac{1}{2} y + \frac{1}{2} y + x + x 2 y + 3 x 100 - 3 x \frac{100 - 3 x}{2}$

Ingat kembali luas permukaan persegi panjang

$L_{p} = = p \cdot l y \cdot x$

Jika $y = \frac{100 - 3 x}{2}$ disubstitusikan pada persamaan di atas maka

$L_{p} = = = y \cdot x (\frac{100 - 3 x}{2}) \cdot x 50 x - \frac{3}{2} x^{2}$

diperoleh fungsi kuadrat dengan $a = - \frac{3}{2}$ dan $b = 50$ sehingga

$x_{mak s} = = = - \frac{b}{2 a} - \frac{50}{2 ( - \frac{3}{2} )} \frac{50}{3}$

diperoleh $x_{mak s} = \frac{50}{3} cm$ dan

$y_{mak s} = = = \frac{100 - 3 x}{2} \frac{100 - 3 ( \frac{50}{3} )}{2} 25 cm$

Dengan demikian, nilai $x$ dan $y$ agar luas permukaan kedua persegi panjang maksimum adalah $x = \frac{50}{3} cm$ dan $y = 25 cm$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

1.0 (1 rating)

Pertanyaan serupa

Luas maksimum persegipanjang pada gambar berikut adalah ....

0.0

Jawaban terverifikasi

Gambar di bawah ini menunjukkan sepetak kebun yang berbentuk persegi panjang ABCD. Kebun itu dipagari dengan kawat sepanjang 20 m . b.luas maksimum ABCD.

5.0

Jawaban terverifikasi

Diketahui sebuah belah ketupat dengan panjang diagonalnya adalah ( 12 − 2 x ) cm dan ( 3 x + 6 ) cm . Tentukan luas maksimum belah ketupat tersebut.

5.0

Jawaban terverifikasi

Apabila P ( x ) mewakili suatu fungsi laba penjualan dari suatu produksi barang ekonomi. yang didefinisikan oleh rumus P ( x ) = 120 x − x 2 , di mana P ( x ) dalam dolar AS dan x dalam satu unit bara...

4.8

Jawaban terverifikasi

Lintasan lembing yang dilemparkan seorang adet mempunyai persamaan h ( t ) = 40 t − 5 t dengan h menunjukkan tinggi lembing dalam meter dan t menunjukkan waktu dalam detik. Tinggi maksimum lintasan le...

4.6

Jawaban terverifikasi