Akar persamaan kuadrat ( a + 1 ) x 2 − 3 a x + 4 a = 0 mempunyai dua akar berbeda dan keduanya lebih besar dari 1, maka nilai a yang memenuhi adalah .... (UM UGM 2017).

Pembahasan

Misal dan adalah akar-akar persamaan kuadrat tersebut. Karena nilai kedua akarnya lebih dari 1, maka diperoleh hasil perhitungan sebagai berikut. dan . Kemudian, diketahui pula bahwa kedua akarnya berbeda, maka diskriminannya harus bernilai positif. Untuk menentukan nilai yang memenuhi, berdasarkan informasi di atas, kita perlu memeriksa 3 kondisi, yaitu penjumlahan akar-akar, perkalian akar-akar, serta nilai diskriminan dari persamaan kuadrat tersebut. (1) Penjumlahan akar-akar Dari dan , karena dan keduanya bernilai positif, maka penjumlahannya juga bernilai positif. Oleh karena itu, kita peroleh sebagai berikut. Kita peroleh pembuat nol pembilangnya adalah dan pembuat nol penyebutnyaadalah . Perhatikan garis bilangan berikut! 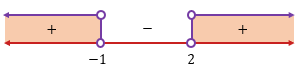Karena tanda pada pertidaksamaannya adalah , maka kita pilih daerah yang bertanda positif, yaitu atau . (2) Perkalian akar-akar Dari (i) dan (ii), karena dan keduanya bernilai positif, maka hasil kalinya juga bernilai positif. Oleh karena itu, kita peroleh sebagai berikut. Kita peroleh pembuat nol pembilangnya adalah dan pembuat nol penyebutnyaadalah . Perhatikan garis bilangan berikut! 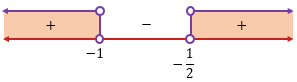Karena tanda pada pertidaksamaannya adalah , maka kita pilih daerah yang bertanda positif, yaitu atau . (3) Nilai diskriminan persamaan kuadrat Ingat bahwa diskriminan dari persamaan kuadrat adalah . Karena persamaan kuadrat memiliki dua akar real berbeda, maka diskriminannya harus bernilai positif. Oleh karena itu, perhatikan perhitungan berikut. Kita peroleh pembuat nolnya adalah atau . Perhatikan garis bilangan berikut! 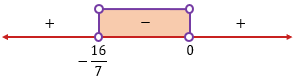Karena tanda pada pertidaksamaannya adalah , maka kita pilih daerah yang bertanda negatif, yaitu . Terakhir, kita cari daerah irisan dari penyelesaian pada poin 1), 2), dan 3) dengan menggabungkan daerahnya pada garis bilangan berikut. 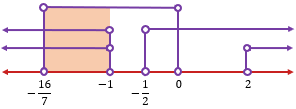Daerah yang memenuhi ketiga kondisi tersebut adalah daerah yang di arsir pada gambar di atas, yaitu . Dengan demikian, nilai yang memenuhi adalah . Jadi, jawaban yang tepat adalah D.