Tentukan suku ke-100 dari barisan di bawah ini! 1 , 3 , 6 , 10 , ...

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah 50 . 050 . Barisan Aritmetika Bertingkat Barisan 1 , 3 , 6 , 10 , ... Beda Barisan Tingkat 1 U 2 ​ − U 1 ​ U 3 ​ − U 2 ​ U 4 ​ − U 3 ​ ​ = = = = = = ​ 3 − 1 2 6 − 3 3 10 − 6 4 ​ Berdasarkan rumus beda barisan di atas ternyata beda barisan pada tingkat pertama belum sama, maka kita cari beda barisan di tingkat kedua. Dengan cara yang sama, sehingga diperoleh: Beda Barisan Tingkat 2 2 , 3 , 4 , ... U 2 ​ − U 1 ​ U 3 ​ − U 2 ​ ​ = = = = ​ 3 − 2 1 4 − 3 1 ​ Diperoleh beda barisan dengan nilai yang sama pada tingkat kedua yaitu 1 . 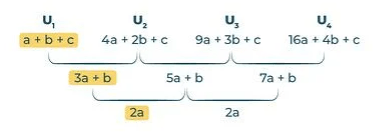Rumus barisan aritmetika bertingkat adalah sebagai berikut: U n ​ = a n 2 + bn + c Pola barisan bertingkat 2 a a ​ = = ​ 1 2 1 ​ ​ 3 a + b 3 ( 2 1 ​ ) + b 2 3 ​ + b b ​ = = = = = ​ 2 2 2 2 − 2 3 ​ 2 1 ​ ​ a + b + c 2 1 ​ + 2 1 ​ + c 1 + c c ​ = = = = = ​ 1 1 1 1 − 1 0 ​ Diperoleh nilai a = 2 1 ​ , b = 2 1 ​ , c = 0 .Substistusi semua nilai ke rumus U n ​ = a n 2 + bn + c untuk menentukan rumus suku ke- n : U n ​ ​ = = = = ​ a n 2 + bn + c ( 2 1 ​ ) n 2 + ( 2 1 ​ ) n + 0 2 1 ​ n 2 + 2 1 ​ n 2 1 ​ ( n 2 + n ) ​ Suku ke-100 adalah: U n ​ U 100 ​ ​ = = = = = ​ 2 1 ​ ( n 2 + n ) 2 1 ​ ( 10 0 2 + 100 ) 2 1 ​ ( 10.000 + 100 ) 2 1 ​ ( 10.100 ) 50.050 ​ Dengan demikian, diperoleh suku ke-100 barisan tersebut adalah 50.050 .