Menentukan koordinat titik potong pasangan garis dengan cara grafik.
1. Menggambar grafik 4x−3y+5=0
- Titik potong dengan sumbu X maka y=0 sehingga
4x−3y+54x−3(0)+54x+54xx=====000−5−45
Titik potong dengan sumbu X: (−45,0)
- Titik potong dengan sumbu Y maka x=0 sehingga
4x−3y+54(0)−3y+5−3y+5−3yy=====000−535
Titik potong dengan sumbu Y : (0,35)
2. Menggambar grafik 3x−7y−2=0
- Titik potong dengan sumbu X maka y=0 sehingga
3x−7y−23x−7(0)−23x−23xx=====000232
Titik potong sumbu X : (32,0)
- Titik potong dengan sumbu Y maka x=0 sehingga
3x−7y−23(0)−7y−2−7y−2−7yy=====0002−72
Titik potong dengan sumbu Y: (0,−72).
Sehingga diperoleh gambar grafik kedua garis sebagai berikut:
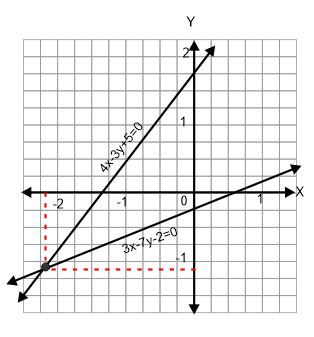
Dari grafik tidak terlihat jelas koordinat titik potong grafik 4x−3y+5=0 dan 3x−7y−2=0 karena hasilnya tidak bulat.
Menentukan koordinat titik potong pasangan garis dengan cara subtitusi.
Diketahui:
4x−3y+53x−7y−2==0...(i)0...(ii)
Perhatikan persamaan (i)
4x−3y+5−3yy===0−4x−534x+5...(iii)
Subtitusikan (iii) ke (ii)
3x−7y−23x−7(34x+5)−29x−7(4x+5)−69x−28x−35−6−19x−41−19xx=======0000041−1941
Subtitusikan nilai x ke (i)
yyyyy=====34x+534(−1941)+53−19164+19953−1969−1923
Sehingga diperoleh titik potong garis 4x−3y+5=0 dan 3x−7y−2=0 adalah (−1941,−1923).
Dengan demikian dengan cara grafik tidak dapat diperoleh titik potong kedua garis dan dengan cara subtitusi diperoleh titik potong garis4x−3y+5=0 dan 3x−7y−2=0 adalah (−1941,−1923).
















