Diketahui pertidaksamaan:

Ditanya:
Nilai optimum fungsi objektif 
Nilai optimum fungsi objektif dari suatu persoalan linear dapat ditentukan dengan metode grafik. Dengan melihat grafik dari fungsi objektif dan batasan-batasannya dapat ditentukan letak titik yang menjadi nilai optimum.
Mencari titik potong terhadap sumbu X (y=0) dan terhadap sumbu Y (x=0)
Titik potong terhadap sumbu  , dengan substitusi
, dengan substitusi 
2x+02xxx====88284(4, 0)
Titik potong terhadap sumbu  , dengan substitusi
, dengan substitusi 
2(0)+y0+yy===888(0, 8)
Titik potong terhadap sumbu  , dengan substitusi
, dengan substitusi 
x+2(0)=8x+0=8x=8(0, 8)
Titik potong terhadap sumbu  , dengan substitusi
, dengan substitusi 
0+2y=82y=8y=28y=4(0, 4)
Dengan demikian, titik potong sumbu  adalah
adalah  dan
dan  sementara titik potong sumbu
sementara titik potong sumbu  adalah
adalah  dan
dan  .
.
Selanjutnya, gambarkan daerah himpunan penyelesaiannya. Ingat :

Daerah himpunan penyelesaian atau arsirannya ke kanan dari sumbu  .
.
Daerah himpunan penyelesaian atau arsirannya ke atas dari sumbu  .
.
Sehingga, grafik pertidaksamaan linear dapat digambarkan seperti berikut:
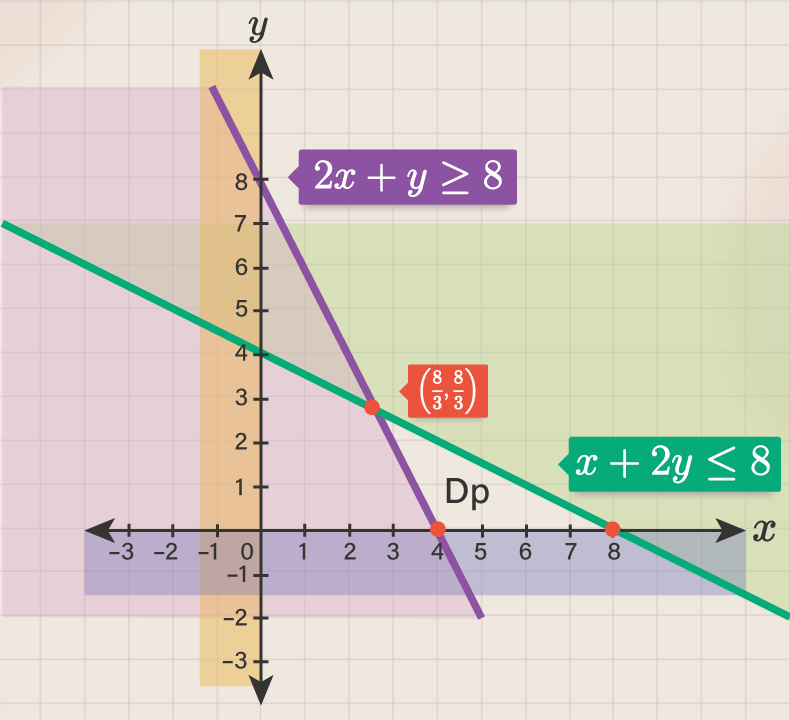
Titik potong pertidaksamaan  dan
dan  dapat ditentukan seperti berikut dengan cara eliminasi-substitusi.
dapat ditentukan seperti berikut dengan cara eliminasi-substitusi.

Substitusikan nilai  ke persamaan
ke persamaan  .
.

Maka, didapat titik potong pertidaksamaan  dan
dan  adalah
adalah  .
.
Dengan menggunakan metode titik pojok, maka didapat titik pojok  dan
dan  .
.
Untuk menentukan nilai maksimum dari fungsi objektif  kita dapat mensubstitusikan titik pojok ke fungsi objektif tersebut.
kita dapat mensubstitusikan titik pojok ke fungsi objektif tersebut.
(4,0)→4+4(0)=4+0=4(8,0)→8+4(0)=8+0=8(38,38)→38+4(38)=38+332=340
Sehingga, nilai optimum fungsi objektif  adalah
adalah .
.
Jadi, jawaban yang tepat adalah D.
















