Pertanyaan

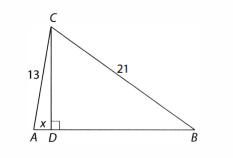
Diketahui segitiga dengan $AC=13,\;CB=21,\;\mathrm{dan}\;AB=20$ . Kita akan menghitung luas segitiga tersebut dengan membagi segitiga tersebut menjadi dua segitiga siku-siku. Untuk itu, tariklah garis $CD$ tegak lurus $AB$ .

a. Misalkan panjang $AD=x$ , tentukan panjang $BD$ .

b. Tuliskan suatu persamaan yang melibatkan $x$ dengan menggunakan segitiga siku-siku $ADC$ dan $DBC$ .

c. Tentukan nilai $x$ .

d. Tentukan panjang $CD$ .

e. Tentukan luas segitiga dengan menggunakan perkalian alas $AB\;$ dan $CD$ .

f. Dengan menggunakan luas segitiga, tentukan panjang garis tegak lurus dari $A$ ke $BC$ .

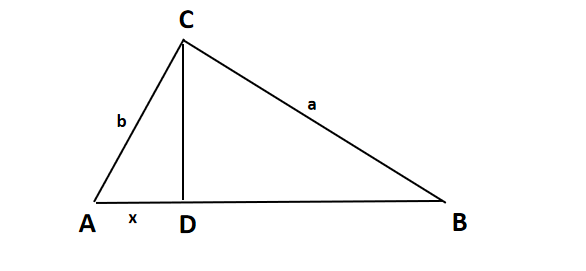
Seperti soal pada nomor (1), misalkan BC = a , A C = b , A B = c . a. Ujilah bahwa panjang x = 2 c b 2 + c 2 − a 2 b. Tentukan panjang C D dengan memanfaatkan segitiga siku-siku A D C . Penuntun: Jangan kuadratkan, tetapi manfaatkan p 2 − q 2 = ( p − q ) ( p + q ) . c. Dengan menuliskan s = 2 a + b + c , maka a + b − c = a + b + c − 2 c = 2 s − 2 c dan lain sebagainya. Perlihatkan bahwa: C D = c 2 s ( s − a ) ( s − b ) ( s − c )

Seperti soal pada nomor (1), misalkan $BC = a, A C = b, A B = c$ .

a. Ujilah bahwa panjang $x = \frac{b ^{2} + c ^{2} - a ^{2}}{2 c}$

b. Tentukan panjang $C D$ dengan memanfaatkan segitiga siku-siku $A D C$ . Penuntun: Jangan kuadratkan, tetapi manfaatkan $p^{2} - q^{2} = (p - q) (p + q)$ .

c. Dengan menuliskan $s = \frac{a + b + c}{2}$ , maka $a + b - c = a + b + c - 2 c = 2 s - 2 c$ dan lain sebagainya. Perlihatkan bahwa:

$C D = \frac{2}{c} s (s - a) (s - b) (s - c)$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Pembahasan

Persoalan tersebut dapat digambarkan sebagai berikut. a. Perhatikan gambar di atas. Dengan menggunakan Pythagoras didapat sebagai berikut. B C 2 a 2 a 2 a 2 2 c x x = = = = = = = C D 2 + B D 2 ( A C 2 − A D 2 ) + B D 2 ( b 2 − x 2 ) + ( c − x ) 2 b 2 − x 2 + c 2 − 2 c x + x 2 b 2 + c 2 − 2 c x b 2 + c 2 − a 2 2 c b 2 + c 2 − a 2 b. Dengan memanfaatkan segitiga siku-siku tersebut, diperoleh sebagai berikut. C D 2 C D = = = A C 2 − A D 2 b 2 − x 2 b 2 − x 2 c. Pertama yakni mencari luas segitiga tersebut. Diperoleh: L △ CD = = = = 2 1 × A B × C D 2 1 × c × C D 2 c × C D c 2 L △ Ingat rumus lain sebagai berikut. L △ = 2 1 ⋅ A B ⋅ A C ⋅ sin A sin 2 A = 1 − cos 2 A s = 2 1 ( a + b + c ) Diperoleh: sin 2 A sin 2 A sin A sin A = = = = = = = = = = = 1 − cos 2 A ( 1 − cos A ) ( 1 + cos A ) ( 1 − 2 b c b 2 + c 2 − a 2 ) ( 1 + 2 b c b 2 + c 2 − a 2 ) ( 2 b c − ( b − c ) 2 + a 2 ) ( 2 b c ( b + c ) 2 − a 2 ) ( 2 b c a 2 − ( b − c ) 2 ) ( 2 b c ( b + c ) 2 − a 2 ) ( 2 b c ( a − b + c ) ( a + b − c ) ) ( 2 b c ( b + c − a ) ( a + b + c ) ) 4 b 2 c 2 ( a − b + c ) ( a + b − c ) ( b + c − a ) ( b + c + a ) b 2 c 2 4 ( 2 a + b + c ) ( 2 a + b + c − a ) ( 2 a + b + c − b ) ( 2 a + b + c − c ) b 2 c 2 4 ( s ) ( s − a ) ( s − b ) ( s − c ) b 2 c 2 4 ( s ) ( s − a ) ( s − b ) ( s − c ) b c 2 ( s ) ( s − a ) ( s − b ) ( s − c ) Substitusi ke persoalan, didapatkan: C D = = = = c 2 L △ c 2 ⋅ 2 1 ⋅ A B ⋅ A C ⋅ sin A c 2 ⋅ 2 1 ⋅ c ⋅ b ⋅ b c 2 s ( s − a ) ( s − b ) ( s − c ) c 2 s ( s − a ) ( s − b ) ( s − c )

Persoalan tersebut dapat digambarkan sebagai berikut.

a. Perhatikan gambar di atas. Dengan menggunakan Pythagoras didapat sebagai berikut.

$B C^{2} a^{2} a^{2} a^{2} 2 c x x = = = = = = = C D^{2} + B D^{2} (A C^{2} - A D^{2}) + B D^{2} (b^{2} - x^{2}) + (c - x)^{2} b^{2} - x^{2} + c^{2} - 2 c x + x^{2} b^{2} + c^{2} - 2 c x b^{2} + c^{2} - a^{2} \frac{b ^{2} + c ^{2} - a ^{2}}{2 c}$

b. Dengan memanfaatkan segitiga siku-siku tersebut, diperoleh sebagai berikut.

$C D^{2} C D = = = A C^{2} - A D^{2} b^{2} - x^{2} b^{2} - x^{2}$

c. Pertama yakni mencari luas segitiga tersebut. Diperoleh:

$L_{△} CD = = = = \frac{1}{2} \times A B \times C D \frac{1}{2} \times c \times C D \frac{c}{2} \times C D \frac{2}{c} L_{△}$

Ingat rumus lain sebagai berikut.

$L_{△} = \frac{1}{2} \cdot A B \cdot A C \cdot sin A sin^{2} A = 1 - cos^{2} A s = \frac{1}{2} (a + b + c)$

Diperoleh:

$sin^{2} A sin^{2} A sin A sin A = = = = = = = = = = = 1 - cos^{2} A (1 - cos A) (1 + cos A) (1 - \frac{b ^{2} + c ^{2} - a ^{2}}{2 b c}) (1 + \frac{b ^{2} + c ^{2} - a ^{2}}{2 b c}) (\frac{- ( b - c ) ^{2} + a ^{2}}{2 b c}) (\frac{( b + c ) ^{2} - a ^{2}}{2 b c}) (\frac{a ^{2} - ( b - c ) ^{2}}{2 b c}) (\frac{( b + c ) ^{2} - a ^{2}}{2 b c}) (\frac{( a - b + c ) ( a + b - c )}{2 b c}) (\frac{( b + c - a ) ( a + b + c )}{2 b c}) \frac{( a - b + c ) ( a + b - c ) ( b + c - a ) ( b + c + a )}{4 b ^{2} c ^{2}} \frac{4}{b ^{2} c ^{2}} (\frac{a + b + c}{2}) (\frac{a + b + c}{2} - a) (\frac{a + b + c}{2} - b) (\frac{a + b + c}{2} - c) \frac{4}{b ^{2} c ^{2}} (s) (s - a) (s - b) (s - c) \frac{4}{b ^{2} c ^{2}} (s) (s - a) (s - b) (s - c) \frac{2}{b c} (s) (s - a) (s - b) (s - c)$

Substitusi ke persoalan, didapatkan:

$C D = = = = \frac{2}{c} L_{△} \frac{2}{c} \cdot \frac{1}{2} \cdot A B \cdot A C \cdot sin A \frac{2}{c} \cdot \frac{1}{2} \cdot c \cdot b \cdot \frac{2}{b c} s (s - a) (s - b) (s - c) \frac{2}{c} s (s - a) (s - b) (s - c)$

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Dari gambar dibawah, panjang BC = ...

3.3

Jawaban terverifikasi

Perhatikan gambar berikut! Tentukan panjang: b. KL

0.0

Jawaban terverifikasi

Sekali lagi, misalkan BC = a , A C = b , dan A B = c . a. Seperti pada soal nomor (2), kita telah melihat bahwa A D = 2 c b 2 + c 2 − a 2 . Berikan dugaan panjang B D , kemudian ujilah. b. ...

0.0

Jawaban terverifikasi

Diketahui segitiga A BC dengan A C = 8 cm , BC = 10 cm , dan A B = 12 cm . b. Jika titik E berada di garis A B sehingga A E = 2 1 EB . Tentukan panjang CE .

0.0

Jawaban terverifikasi

Berdasar gambar di bawah ini, keliling segitiga ABC adalah ...

4.4

Jawaban terverifikasi