Pertanyaan

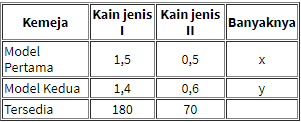
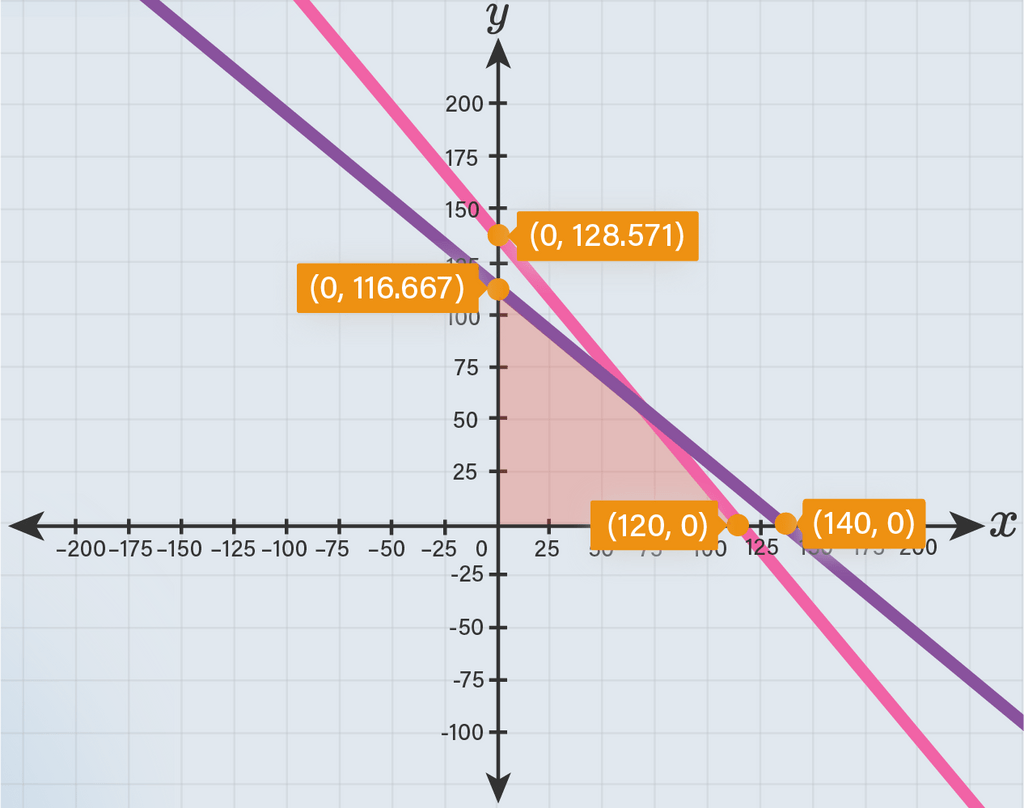
Seorang tukang jahit ingin membuat 2 model kemeja yang menggunakan 2 jenis kain. Kemeja model pertama memerlukan 1 , 5 meter kain jenis pertama dan 0 , 5 meter kain jenis kedua. Sementara kemeja model kedua memerlukan 1 , 4 meter kain jenis pertama dan 0 , 6 meter kain jenis kedua. Kain jenis pertama yang tersedia ada 180 meter dan kain jenis kedua ada 70 meter. Misal banyak kemeja model pertama yang akan dibuat = x dan kemeja model kedua = y , buatlah model matematika yang sesuai dengan masalah tersebut, kemudian gambarkanlah daerah penyelesaiannya pada grafik Cartesius.

Seorang tukang jahit ingin membuat $2$ model kemeja yang menggunakan $2$ jenis kain. Kemeja model pertama memerlukan $1, 5$ meter kain jenis pertama dan $0, 5$ meter kain jenis kedua. Sementara kemeja model kedua memerlukan $1, 4$ meter kain jenis pertama dan $0, 6$ meter kain jenis kedua. Kain jenis pertama yang tersedia ada $180$ meter dan kain jenis kedua ada $70$ meter. Misal banyak kemeja model pertama yang akan dibuat $= x$ dan kemeja model kedua $= y$ , buatlah model matematika yang sesuai dengan masalah tersebut, kemudian gambarkanlah daerah penyelesaiannya pada grafik Cartesius.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

model matematika yang sesuai dengan masalah tersebut adalah 1 , 5 x + 1 , 4 y ≤ 180 , 0 , 5 x + 0 , 6 y ≤ 70 , x ≥ 0 dan y ≥ 0 dan gambar daerah penyelesaian seperti pada gambar diatas.

model matematika yang sesuai dengan masalah tersebut adalah

1, 5 x + 1, 4 y \leq 180

0, 5 x + 0, 6 y \leq 70

x \geq 0

dan

y \geq 0

dan gambar daerah penyelesaian seperti pada gambar diatas.

Pembahasan

Masalah pada soal dapat disajikan dalam tabel berikut, Banyak kemeja model pertama = x dan kemeja model kedua = y . Jumlah kain jenis I yang tersedia = 180 , maka 1 , 5 x + 1 , 4 y ≤ 180 Jumlah kain jenis II yang tersedia = 70 , maka 0 , 5 x + 0 , 6 y ≤ 70 Banyaknya kemeja harus lebih dari nol maka x ≥ 0 dan y ≥ 0 Di dapatkan model matematika 1 , 5 x + 1 , 4 y ≤ 180 , 0 , 5 x + 0 , 6 y ≤ 70 , x ≥ 0 dan y ≥ 0 . a. 1 , 5 x + 1 , 4 y ≤ 180 1 , 5 x + 1 , 4 y = 180 Jika x = 0 maka y = 128 , 6 Jika y = 0 maka x = 120 Di dapatkan dua titik yaitu ( 120 , 0 ) dan ( 0 , 128 , 6 ) . b. 0 , 5 x + 0 , 6 y ≤ 70 0 , 5 x + 0 , 6 y = 70 Jika x = 0 maka y = 116 , 7 Jika y = 0 maka x = 140 Di dapatkan dua titik yaitu ( 140 , 0 ) dan ( 0 , 116 , 7 ) . Tentukan daerah penyelesaian mennggunakan titik uji (Misal titik uji ( 0 , 0 ) ). 1 , 5 x + 1 , 4 y ≤ 180 1 , 5 x + 1 , 4 y 1 , 5 ⋅ 0 + 1 , 4 ⋅ 0 0 ≤ ≤ ≤ 180 180 180 ( benar ) Karena benar bahwa 0 ≤ 180 , maka daerah yang memuat titik ( 0 , 0 ) merupakan daerah penyelesaian dari 1 , 5 x + 1 , 4 y ≤ 180 . 0 , 5 x + 0 , 6 y ≤ 70 0 , 5 x + 0 , 6 y 0 , 5 ⋅ 0 + 0 , 6 ⋅ 0 0 ≤ ≤ ≤ 70 70 70 ( benar ) Karena benar bahwa 0 ≤ 70 , maka daerah yang memuat titik ( 0 , 0 ) merupakan daerah penyelesaian dari 0 , 5 x + 0 , 6 y ≤ 70 . Sehingga gambar daerah penyelesaiannya adalah: Jadi, model matematika yang sesuai dengan masalah tersebut adalah 1 , 5 x + 1 , 4 y ≤ 180 , 0 , 5 x + 0 , 6 y ≤ 70 , x ≥ 0 dan y ≥ 0 dan gambar daerah penyelesaian seperti pada gambar diatas.

Masalah pada soal dapat disajikan dalam tabel berikut,

Banyak kemeja model pertama $= x$ dan kemeja model kedua $= y$ .
Jumlah kain jenis I yang tersedia $= 180$ , maka $1, 5 x + 1, 4 y \leq 180$
Jumlah kain jenis II yang tersedia $= 70$ , maka $0, 5 x + 0, 6 y \leq 70$
Banyaknya kemeja harus lebih dari nol maka $x \geq 0$ dan $y \geq 0$

Di dapatkan model matematika $1, 5 x + 1, 4 y \leq 180$ , $0, 5 x + 0, 6 y \leq 70$ , $x \geq 0$ dan $y \geq 0$ .

a. $1, 5 x + 1, 4 y \leq 180$

$1, 5 x + 1, 4 y = 180$

Jika $x = 0$ maka $y = 128, 6$
Jika $y = 0$ maka $x = 120$

Di dapatkan dua titik yaitu $(120, 0)$ dan $(0, 128, 6)$ .

b. $0, 5 x + 0, 6 y \leq 70$

$0, 5 x + 0, 6 y = 70$

Jika $x = 0$ maka $y = 116, 7$
Jika $y = 0$ maka $x = 140$

Di dapatkan dua titik yaitu $(140, 0)$ dan $(0, 116, 7)$ .

Tentukan daerah penyelesaian mennggunakan titik uji (Misal titik uji $(0, 0)$ ).

$1, 5 x + 1, 4 y \leq 180$

$1, 5 x + 1, 4 y 1, 5 \cdot 0 + 1, 4 \cdot 0 0 \leq \leq \leq 180180 180 (benar)$

Karena benar bahwa $0 \leq 180$ , maka daerah yang memuat titik $(0, 0)$ merupakan daerah penyelesaian dari $1, 5 x + 1, 4 y \leq 180$ .

$0, 5 x + 0, 6 y \leq 70$

$0, 5 x + 0, 6 y 0, 5 \cdot 0 + 0, 6 \cdot 0 0 \leq \leq \leq 7070 70 (benar)$

Karena benar bahwa $0 \leq 70$ , maka daerah yang memuat titik $(0, 0)$ merupakan daerah penyelesaian dari $0, 5 x + 0, 6 y \leq 70$ .

Sehingga gambar daerah penyelesaiannya adalah:

Jadi, model matematika yang sesuai dengan masalah tersebut adalah $1, 5 x + 1, 4 y \leq 180$ , $0, 5 x + 0, 6 y \leq 70$ , $x \geq 0$ dan $y \geq 0$ dan gambar daerah penyelesaian seperti pada gambar diatas.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.9 (20 rating)

Yua Nusa Guna Indardi

YEY AKU CINTA BA

SyifaNN _Untsa

Makasih ❤️ Pembahasan lengkap banget

Nezta

Pembahasan lengkap banget

Atikah

Ini yang aku cari!

nurlaila

Pembahasan lengkap banget

Pertanyaan serupa

Ibu akan membuat dua jenis kue, kue tart dan kue lapis. Untuk membuat 1 kue tart, dibutuhkan 10 gram tepung dan 15 gram gula. Untuk membuat 1 kue lapis, dibutuhkan 20 gram tepung dan 10 gram gula. Ibu...

3.6

Jawaban terverifikasi

Budi membeli 2 buah roti keju dan 3 roti cokelat seharga Rp 34.500 , 00 . Andi membeli 5 buah roti keju dan 8 roti cokelat seharga Rp 85.500 , 00 . Keduanya berharap setelah ditawar, harga yang harus ...

5.0

Jawaban terverifikasi

Grafik y = x 2 − 2 x + 3 berada di bawah grafik y = − x 2 + 4 x + 23 untuk ...

5.0

Jawaban terverifikasi

Seorang manager ingin merencanakan pemasangan iklan produknya, untuk mencapai 7.200.000 calon pembeli yang di antaranya terdapat 640.000 berpenghasilan di atas Rp 45.000.000 , 00 pertahun. Pembaca yan...

5.0

Jawaban terverifikasi

Grafik y = x 2 − 2 x + 3 berada di bawah grafik y = − x 2 + 4 x + 23 untuk ...

5.0

Jawaban terverifikasi