Iklan
Pertanyaan
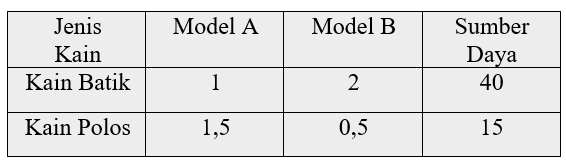
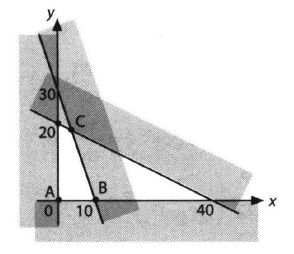
Seorang penjahit akan membuat 2 modelpakaian. Dia mempunyai persediaan kainbatik 40 meter dan kain polos 15 meter .Model A memerlukan 1 meter kain batikdan 1 , 5 meter kain polos, sedang model B memerlukan 2 meter kain batik dan 0 , 5 meter kain polos. Maksimum banyakpakaian yang mungkin dapat dibuat adalah …
Seorang penjahit akan membuat model pakaian. Dia mempunyai persediaan kain batik dan kain polos .Model memerlukan kain batik dan kain polos, sedang model memerlukan kain batik dan kain polos. Maksimum banyak pakaian yang mungkin dapat dibuat adalah
Iklan
W. Wati
Master Teacher
4
4.8 (22 rating)
Nayla Hidayati Nakhila
Bantu banget
raisa dika imtiyaz
Pembahasan lengkap banget
Fitari Meysa Fitri
Makasih ❤️ Bantu banget Ini yang aku cari! Pembahasan lengkap banget
Levia Aryani
Pembahasan lengkap banget
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia