Ingat soal ini merupakan konsep optimisasi program linear.
Dari soal diminta mencari nilai maksimum fungsi objektif (tujuan) f(x, y)=4x+3y dengan kendala 2x+3y≤18, x≥3, dan y≥2. Berikut langkah-langkah penyelesaian :
1. Menggambar daerah penyelesaian
- titik potong garis 2x+3y=18 dengan sumbu x dan sumbu y
jika x=0, maka :
(2×0)+3y3yy===1818318=6
maka titik potong adalah (0, 6)
jika y=0, maka :
2x+(3×0)2xx===1818218=9
maka titik potong adalah (9, 0)
Selanjutnya untuk uji titik diambil (0, 0) sehingga (2×0)+(3×0)=0<18 (benar)
Diperoleh daerah penyelesaian sebagai berikut :
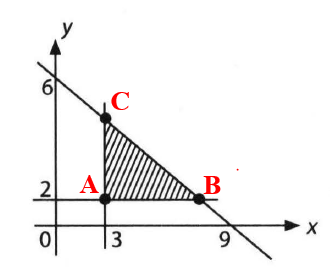
2. Menentukan titik potong
Titik potong pada C (antara x=3 dan 2x+3y=18) :
Jika x=3 maka :
(2×3)+3y3yy===1818−6=12312=4
maka titik potong adalah (3, 4).
Titik potong B (antara y=2 dan 2x+3y=18) :
Jika y=2 maka :
2x+(3×2)2xx===1818−6=12212=6
maka titik potong adalah (6, 2).
titik potong A (antara x=3 dan y=2) adalah A(3, 2).
3. Menentukan f(x, y)
f(x, y)=4x+3y :
A(3, 2)⇒f(3, 2)=(4×3)+(3×2)=18B(6, 2)⇒f(6, 2)=(4×6)+(3×2)=30A(3, 4)⇒f(3, 4)=(4×3)+(3×4)=24
Jadi nilai fmaks=30.
Oleh karena itu, jawaban yang benar adalah B.
















