Iklan
Pertanyaan
Segitiga PQR siku-siku di R. 2 cos α − sin β = ....
Segitiga PQR siku-siku di R.
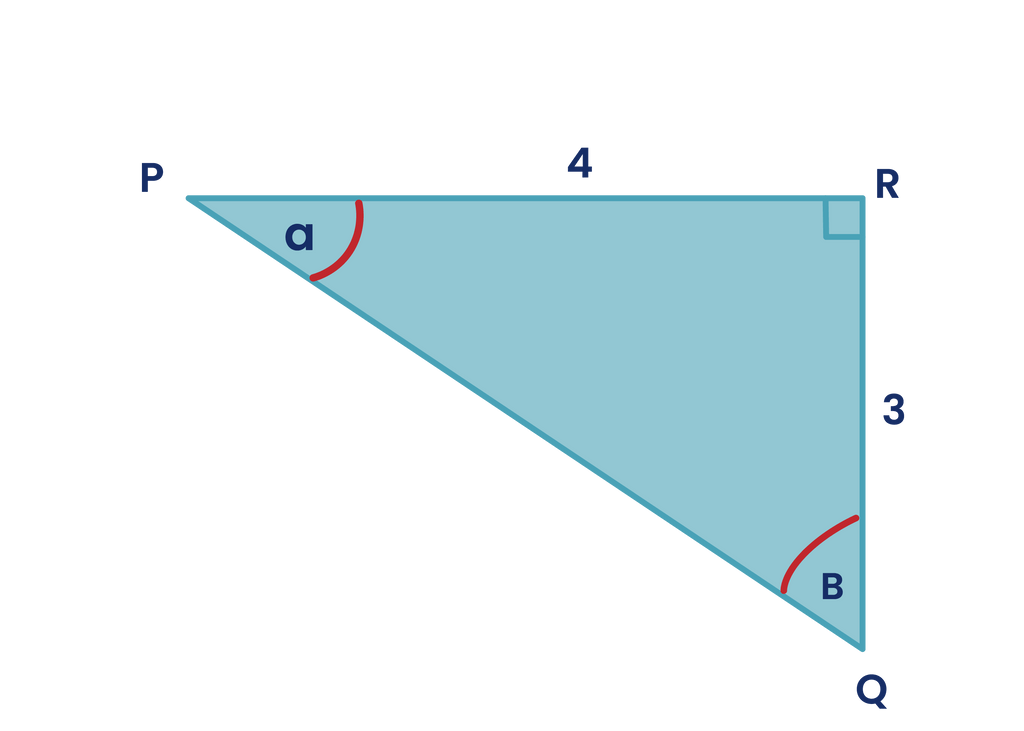
....
Iklan
IK
I. Kumaralalita
Master Teacher
Mahasiswa/Alumni Universitas Gadjah Mada
Jawaban terverifikasi
4
4.5 (32 rating)
Z
Zahra
Jawaban tidak sesuai
SW
Salsabila Wahyu Lestari
Jawaban tidak sesuai Pembahasan terpotong Pembahasan tidak menjawab soal
A
Anon
Makasih ❤️
da
defannie aura istri
Ini yang aku cari!
DR
Darien Rahma Syauqiah
Mudah dimengerti
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia















