Pertanyaan

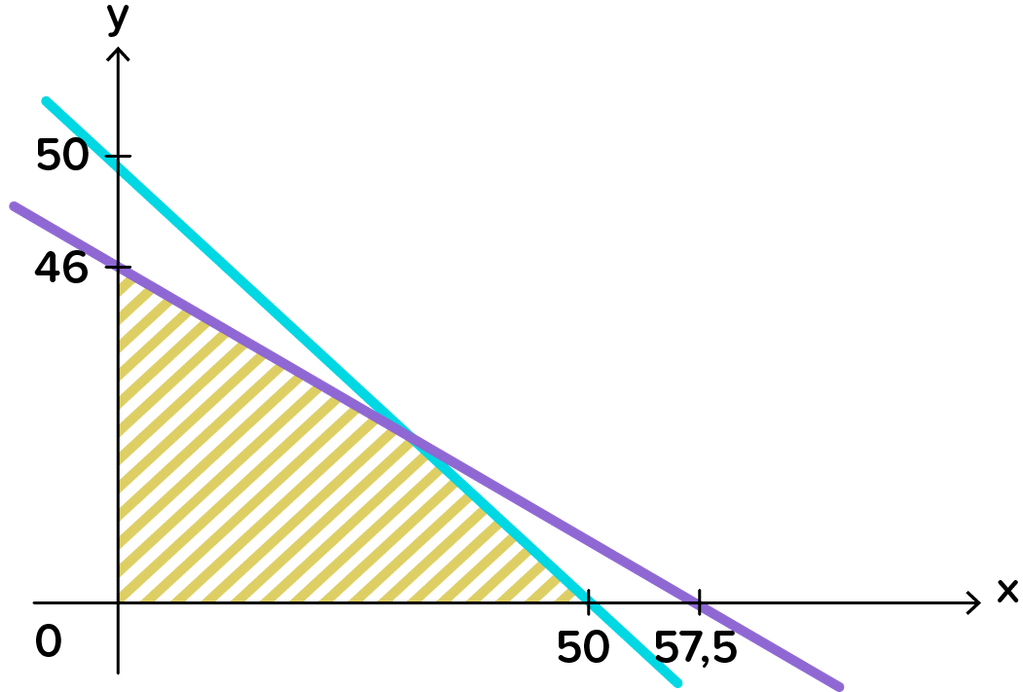
Sebuah toko sepeda menyediakan dua jenis sepeda, yaitu sepeda dengan setang dan sepeda tanpa setang yang harganya berturut-turut Rp400.000,00 dan RP500.000,00. Kapasitas toko tersebut tidak lebih dari 50 sepeda. Uang yang tersedia untuk modal adalah Rp23.000.000,00. Gambarlah daerah penyelesaian sistem pertidaksamaan linear agar keuntungan maksimum.

Sebuah toko sepeda menyediakan dua jenis sepeda, yaitu sepeda dengan setang dan sepeda tanpa setang yang harganya berturut-turut Rp400.000,00 dan RP500.000,00. Kapasitas toko tersebut tidak lebih dari 50 sepeda. Uang yang tersedia untuk modal adalah Rp23.000.000,00. Gambarlah daerah penyelesaian sistem pertidaksamaan linear agar keuntungan maksimum. $\;$

N. Puspita

Master Teacher

Jawaban terverifikasi

Pembahasan

Misalkan: sepeda dengan setang sepeda tanpa setang Kapasitas toko tersebut tidak lebih dari 50 sepeda, sehingga pertidaksamaannya: Uang yang tersedia untuk modal adalah Rp23.000.000,00. Maka, gambar daerah penyelesaiannya: memotong di dan memotong di: Jadi, gambarlah daerah penyelesaian sistem pertidaksamaan linear agar keuntungan maksimum adalah sebagai berikut.

Misalkan:

sepeda dengan setang
sepeda tanpa setang

Kapasitas toko tersebut tidak lebih dari 50 sepeda, sehingga pertidaksamaannya:

x plus y less or equal than 50

Uang yang tersedia untuk modal adalah Rp23.000.000,00.

table attributes columnalign right center left columnspacing 0px end attributes row cell 400.000 x plus 500.000 y end cell less or equal than cell 23.000.000 end cell row cell 4 x plus 5 y end cell less or equal than 230 end table

Maka, gambar daerah penyelesaiannya:

memotong di dan
memotong di:

table attributes columnalign right center left columnspacing 0px end attributes row blank rightwards arrow cell y equals 0 end cell row cell 4 x plus 5 y end cell equals 230 row cell 4 x plus 5 times 0 end cell equals 230 row cell 4 x end cell equals 230 row x equals cell 57 comma 5 end cell end table

table attributes columnalign right center left columnspacing 0px end attributes row blank rightwards arrow cell x equals 0 end cell row cell 4 x plus 5 y end cell equals 230 row cell 4 times 0 plus 5 y end cell equals 230 row cell 5 y end cell equals 230 row y equals 46 end table

Jadi, gambarlah daerah penyelesaian sistem pertidaksamaan linear agar keuntungan maksimum adalah sebagai berikut.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Suatu perusahaan transportasi harus mendistribusikan 1.200 paket (yang besarnya sama) melalui dua truk pengangkut. Truk 1 memuat 200 paket untuk setiap pengangkutan dan truk 2 memuat 80 paket untuk se...

4.5

Jawaban terverifikasi

PT Usaha Rotanindo di Cirebonmemproduksi dua jenis mebel rotan, yaitujenis kursi dan meja. Kapasitas produksiperusahaan tidak kurang dari 1.000 unitbarang per bulan. Dari bagian marketing,diperoleh in...

5.0

Jawaban terverifikasi

Seorang pemborong mempunyaipersediaan 100 kaleng cat warna hijaudan 240 kaleng cat warna abu-abu.Pemborong tersebut mendapat order untuk mengecat ruang tamu dan ruang tidur disuatu gedung. Setelah dik...

3.0

Jawaban terverifikasi

Seorang pedagang ponsel memilikimodal sebesar Rp 49.600.000 , 00 untukmenjual dua jenis ponsel sebanyak-banyaknya 25 unit. Pedagang tersebutakan menjual ponsel jenis android danjenis biasa dengan harg...

4.7

Jawaban terverifikasi

Harga bawang merah Rp 25.000,00 per kg dan harga bawang putih Rp 50.000,00 per kg. Seorang pedangan hanya mempunyai modal Rp 20.000.000,00 dan kiosnnya hanya dapat memuat tidak lebih dari 600 kg denga...

3.0

Jawaban terverifikasi