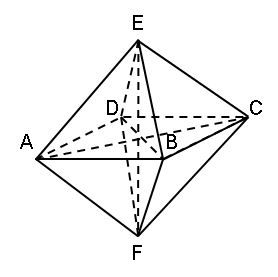
Perhatikan gambar berikut! Sebuah kristal kalium karbonat yang diamati melalui sebuah mikroskop memiliki bentuk sebuah segidelapan seperti yang ditunjukkan dalam gambar. Titik-titik sudutnya relatif terhadap satu sistem sumbu koordinat yang sesuai adalah A ( 1 , − 5 , 2 ) , B ( 6 , − 3 , 4 ) , C ( 7 , 1 , 0 ) , D ( 2 , − 1 , − 2 ) , E ( − 4 , 9 , 10 ) dan F ( 12 , − 13 , − 8 ) . Tunjukkan bahwa diagonal ruang AC dan EF dari kristal ini saling berpotongan tegak lurus.

Pembahasan

Jawaban yang benar adalah terbukti bahwadiagonal ruang AC dan EF dari kristal tersebut saling berpotongan tegak lurus di titik ( 4 , − 2 , 1 ) . Ingat bahwa vektor posisi suatu titik, merupakan vektor dari titik asal hingga ke titik yang dimaksud. Sedangkan vektor posisititik A ( a 1 ​ , a 2 ​ , a 3 ​ ) terhadap titik B ( b 1 ​ , b 2 ​ , b 3 ​ ) , yaitu: BA = ( a 1 ​ , a 2 ​ , a 3 ​ ) − ( b 1 ​ , b 2 ​ , b 3 ​ ) Perkalian vektor u ( u 1 ​ , u 2 ​ , u 3 ​ ) dengan skalar k dapat dilakukan sebagaimana rumus berikut: k u ​ = = ​ k ( u 1 ​ , u 2 ​ , u 3 ​ ) ( k u 1 ​ , k u 2 ​ , k u 3 ​ ) ​ Vektor AC dapat diperoleh dari perhitungan berikut: AC ​ = = = ​ ( 7 , 1 , 0 ) − ( 1 , − 5 , 2 ) ( 7 − 1 , 1 − ( − 5 ) , 0 − 2 ) ( 6 , 6 , − 2 ) ​ Vektor EF dapat diperoleh dari perhitungan berikut: EF ​ = = = ​ ( 12 , − 13 , − 8 ) − ( − 4 , 9 , 10 ) ( 12 − ( − 4 ) , − 13 − 9 , − 8 − 10 ) ( 16 , − 22 , − 18 ) ​ Misalkan titik O adalah titik asal, titik tengah AC adalah G, dan titik tengah EF adalah H. Untuk menunjukkan bahwa diagonal ruang AC dan EF saling berpotongan, maka dapat ditunjukkan bahwa titik G dan titik H adalah titik yang sama. Vektor posisi titik G dapat diperoleh dari penjumlahan vektor dengan metode segitiga, yaitu: OG ​ = = = = = = ​ OA + AG ( 1 , − 5 , 2 ) + 2 1 ​ AC ( 1 , − 5 , 2 ) + 2 1 ​ ( 6 , 6 , − 2 ) ( 1 , − 5 , 2 ) + ( 3 , 3 , − 1 ) ( 1 + 3 , − 5 + 3 , 2 − 1 ) ( 4 , − 2 , 1 ) ​ Vektor posisititik H dapat diperoleh dari penjumlahan vektor dengan metode segitiga, yaitu: OH ​ = = = = = = ​ OE + EH ( − 4 , 9 , 10 ) + 2 1 ​ EF ( − 4 , 9 , 10 ) + 2 1 ​ ( 16 , − 22 , − 18 ) ( − 4 , 9 , 10 ) + ( 8 , − 11 , − 9 ) ( − 4 + 8 , 9 − 11 , 10 − 9 ) ( 4 , − 2 , 1 ) ​ Karena OG = OH , maka titik G dan titik H merupakan titik yang sama. Sehingga, diagonal ruang AC dan EF dari kristal tersebut saling berpotongan di titik ( 4 , − 2 , 1 ) . Selanjutnya, akan dibuktikan bahwa diagonal ruang AC dan EF saling tegak lurus. Ingat bahwa hasil perkalian dot product dua vektor u = ( a , b , c ) dan v = ( x , y , z ) yang saling tegak lurus adalahsebagai berikut: u ⋅ v a x + b y + cz ​ = = ​ 0 0 ​ Sehingga untuk membuktikan diagonal ruang AC dan EF saling tegak lurus, maka perlu ditunjukkan bahwa hasil perkalian dot product antara vektor AC dan EF adalah 0. Berikut adalah hasil kali dot product kedua vektor tersebut: AC ⋅ EF ​ = = = = ​ ( 6 , 6 , − 2 ) ⋅ ( 16 , − 22 , − 18 ) ( 6 ) ( 16 ) + ( 6 ) ( − 22 ) + ( − 2 ) ( − 18 ) 96 − 132 + 36 0 ​ Karena hasil kali dot productvektor AC dan EF adalah 0, maka diagonal ruang AC dan EFsaling tegak lurus. Dengan demikian, diagonal ruang AC dan EF dari kristal tersebut saling berpotongan tegak lurus di titik ( 4 , − 2 , 1 ) .