Pertanyaan

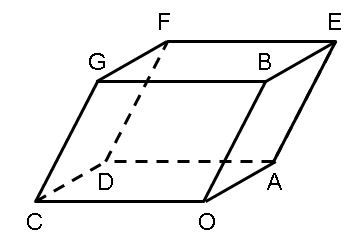
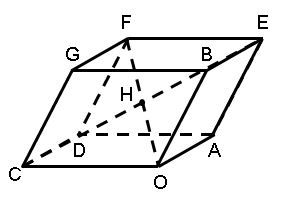
Gambar OADC.BEFG adalah paralelpipedum yaitu padatan dengan enam sisi. Setiap sisi jajargenjang yang berseberangan kongruen. O adalah titik asal. A, B, dan C masing-masing memiliki vektor posisi ⎝ ⎛ 1 0 0 ⎠ ⎞ , ⎝ ⎛ 2 1 2 ⎠ ⎞ , dan ⎝ ⎛ − 3 2 1 ⎠ ⎞ . Tentukan vektor posisi titik tengah OF dan jelaskan titik potong antara diagonal ruang OF dan CE.

Gambar OADC.BEFG adalah paralelpipedum yaitu padatan dengan enam sisi. Setiap sisi jajargenjang yang berseberangan kongruen. O adalah titik asal. A, B, dan C masing-masing memiliki vektor posisi $⎝ ⎛ 100 ⎠ ⎞$ , $⎝ ⎛ 212 ⎠ ⎞$ , dan $⎝ ⎛ - 3 21 ⎠ ⎞$ .

Tentukan vektor posisi titik tengah $OF$ dan jelaskan titik potong antara diagonal ruang OF dan CE.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

vektor posisi titik tengah OF adalah OH = ⎝ ⎛ 0 2 3 2 3 ⎠ ⎞ dan vektor posisi tersebut menunjukkan posisititik potong antara diagonal ruang OD dan CE di titik H.

vektor posisi titik tengah

OF

adalah

OH = ⎝ ⎛ 0 \frac{3}{2} \frac{3}{2} ⎠ ⎞

dan vektor posisi tersebut menunjukkan posisi titik potong antara diagonal ruang OD dan CE di titik H.

Pembahasan

Jawaban yang benar atas pertanyaan tersebut adalah OH = ⎝ ⎛ 0 2 3 2 3 ⎠ ⎞ dan vektor posisi tersebut menunjukkan posisititik potong antara diagonal ruang OD dan CE di titik H. Iustrasi: Ingat bahwa vektor posisi suatu titik, merupakan vektor dari titik asal hingga ke titik yang dimaksud. Sedangkan perkalian vektor u = ⎝ ⎛ u 1 u 2 u 3 ⎠ ⎞ dengan skalar k dapat dilakukan sebagaimana rumus berikut: k u = k ⎝ ⎛ u 1 u 2 u 3 ⎠ ⎞ = ⎝ ⎛ k u 1 k u 2 k u 3 ⎠ ⎞ Diketahui bahwa AD = OC dan AE = OB . Panjang OF dan CE dapat diperoleh dari penjumlahan vektor metode poligonberikut: OF = = = OA + AD + DF ⎝ ⎛ 1 0 0 ⎠ ⎞ + ⎝ ⎛ 2 1 2 ⎠ ⎞ + ⎝ ⎛ − 3 2 1 ⎠ ⎞ ⎝ ⎛ 0 3 3 ⎠ ⎞ dan CE = = = = = CO + OA + AE − OC + OA + OB − ⎝ ⎛ − 3 2 1 ⎠ ⎞ + ⎝ ⎛ 1 0 0 ⎠ ⎞ + ⎝ ⎛ 2 1 2 ⎠ ⎞ ⎝ ⎛ 3 − 2 − 1 ⎠ ⎞ + ⎝ ⎛ 1 0 0 ⎠ ⎞ + ⎝ ⎛ 2 1 2 ⎠ ⎞ ⎝ ⎛ 6 − 1 1 ⎠ ⎞ Misalkan titik tengah OF adalah H. Sehingga vektor posisi titik tengah OF adalah vektor OH . Vektor dapat diperoleh melalui perhitunganberikut: OH = = = 2 1 OF 2 1 ⎝ ⎛ 0 3 3 ⎠ ⎞ ⎝ ⎛ 0 2 3 2 3 ⎠ ⎞ Titik potong antara diagonal ruang OF dan CE adalah titik tengah garis OF dan garis CE dimana titik tersebut terletak di titik H. Untuk menunjukkan bahwa vektor posisi OH merupakan lokasi titik potong diagonal ruang OF dan CE, maka perlu menentukan vektor posisi OH berdasarkan vektor CE sebagai berikut: OH = = = = = OC + CH OC + 2 1 CE ⎝ ⎛ − 3 2 1 ⎠ ⎞ + 2 1 ⎝ ⎛ 6 − 1 1 ⎠ ⎞ ⎝ ⎛ − 3 2 1 ⎠ ⎞ + ⎝ ⎛ 3 − 2 1 2 1 ⎠ ⎞ ⎝ ⎛ 0 2 3 2 3 ⎠ ⎞ Karena dihasilkan nilai vektor posisi yang sama dari diagonal CE dan OF, maka kedua garis tersebut terbukti berpotongan di tengah yaitu di titik H. Dengan demikian, vektor posisi titik tengah OF adalah OH = ⎝ ⎛ 0 2 3 2 3 ⎠ ⎞ dan vektor posisi tersebut menunjukkan posisititik potong antara diagonal ruang OD dan CE di titik H.

Jawaban yang benar atas pertanyaan tersebut adalah $OH = ⎝ ⎛ 0 \frac{3}{2} \frac{3}{2} ⎠ ⎞$ dan vektor posisi tersebut menunjukkan posisi titik potong antara diagonal ruang OD dan CE di titik H.

Iustrasi:

Ingat bahwa vektor posisi suatu titik, merupakan vektor dari titik asal hingga ke titik yang dimaksud. Sedangkan perkalian vektor $u = ⎝ ⎛ u_{1} u_{2} u_{3} ⎠ ⎞$ dengan skalar $k$ dapat dilakukan sebagaimana rumus berikut:

$k u = k ⎝ ⎛ u_{1} u_{2} u_{3} ⎠ ⎞ = ⎝ ⎛ k u_{1} k u_{2} k u_{3} ⎠ ⎞$

Diketahui bahwa $AD = OC$ dan $AE = OB$ . Panjang $OF$ dan $CE$ dapat diperoleh dari penjumlahan vektor metode poligon berikut:

$OF = = = OA + AD + DF ⎝ ⎛ 100 ⎠ ⎞ + ⎝ ⎛ 212 ⎠ ⎞ + ⎝ ⎛ - 3 21 ⎠ ⎞ ⎝ ⎛ 033 ⎠ ⎞$

dan

$CE = = = = = CO + OA + AE - OC + OA + OB - ⎝ ⎛ - 3 21 ⎠ ⎞ + ⎝ ⎛ 100 ⎠ ⎞ + ⎝ ⎛ 212 ⎠ ⎞ ⎝ ⎛ 3 - 2 - 1 ⎠ ⎞ + ⎝ ⎛ 100 ⎠ ⎞ + ⎝ ⎛ 212 ⎠ ⎞ ⎝ ⎛ 6 - 1 1 ⎠ ⎞$

Misalkan titik tengah $OF$ adalah H. Sehingga vektor posisi titik tengah $OF$ adalah vektor $OH$ . Vektor dapat diperoleh melalui perhitungan berikut:

$OH = = = \frac{1}{2} OF \frac{1}{2} ⎝ ⎛ 033 ⎠ ⎞ ⎝ ⎛ 0 \frac{3}{2} \frac{3}{2} ⎠ ⎞$

Titik potong antara diagonal ruang OF dan CE adalah titik tengah garis OF dan garis CE dimana titik tersebut terletak di titik H. Untuk menunjukkan bahwa vektor posisi $OH$ merupakan lokasi titik potong diagonal ruang OF dan CE, maka perlu menentukan vektor posisi $OH$ berdasarkan vektor $CE$ sebagai berikut:

$OH = = = = = OC + CH OC + \frac{1}{2} CE ⎝ ⎛ - 3 21 ⎠ ⎞ + \frac{1}{2} ⎝ ⎛ 6 - 1 1 ⎠ ⎞ ⎝ ⎛ - 3 21 ⎠ ⎞ + ⎝ ⎛ 3 - \frac{1}{2} \frac{1}{2} ⎠ ⎞ ⎝ ⎛ 0 \frac{3}{2} \frac{3}{2} ⎠ ⎞$

Karena dihasilkan nilai vektor posisi yang sama dari diagonal CE dan OF, maka kedua garis tersebut terbukti berpotongan di tengah yaitu di titik H.

Dengan demikian, vektor posisi titik tengah $OF$ adalah $OH = ⎝ ⎛ 0 \frac{3}{2} \frac{3}{2} ⎠ ⎞$ dan vektor posisi tersebut menunjukkan posisi titik potong antara diagonal ruang OD dan CE di titik H.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Perhatikan gambar berikut! Sebuah kristal kalium karbonat yang diamati melalui sebuah mikroskop memiliki bentuk sebuah segidelapan seperti yang ditunjukkan dalam gambar. Titik-titik sudutnya rel...

0.0

Jawaban terverifikasi

Perhatikan gambar berikut! Sebuah kristal kalium karbonat yang diamati melalui sebuah mikroskop memiliki bentuk sebuah segidelapan seperti yang ditunjukkan dalam gambar. Titik-titik sudutnya rel...

0.0

Jawaban terverifikasi

Tentukanlah hasil penjumlahan dan pengurangan vektor-vektor berikut secara geometri menggunakan metode segitiga/ jajargenjang/ poligon dan secara aljabar. 7. b → + 2 c → + 3 d →

4.0

Jawaban terverifikasi

Tentukanlah hasil penjumlahan dan pengurangan vektor-vektor berikut secara geometri menggunakan metode segitiga/ jajargenjang/ poligon dan secara aljabar. 7. b → + 2 c → + 3 d →

4.0

Jawaban terverifikasi

Diketahui vektor OP = ( 3 , − 2 ) , OQ = ( − 1 , 5 ) , OR = ( 7 , 4 ) . Jika vektor a mewakili PQ , vektor b mewakili QR , dan vektor c mewakili PR ,hitunglah 2 b − 3 c + a !

0.0

Jawaban terverifikasi