Pertanyaan

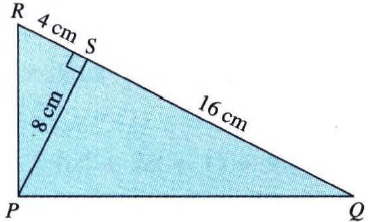
Perhatikan gambar berikut! Pada △ PQR di atas, panjang RS = 4 cm , PS = 8 cm , dan QS = 16 cm . a. Hitunglah panjang PQ ! b. Hitunglah panjang PR ! c. Tunjukkan bahwa △ PQR siku-siku di P !

Perhatikan gambar berikut!

Pada $△ PQR$ di atas, panjang $RS = 4 cm$ , $PS = 8 cm$ , dan $QS = 16 cm$ .
a. Hitunglah panjang $PQ$ !
b. Hitunglah panjang $PR$ !
c. Tunjukkan bahwa $△ PQR$ siku-siku di $P$ !

E. Lestari

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Jawaban

karena QR 2 = PQ 2 + PR 2 maka △ PQR adalah segitiga siku-siku di P .

karena

QR^{2} = PQ^{2} + PR^{2}

maka

△ PQR

adalah segitiga siku-siku di

P

Pembahasan

Ingat! Rumus Pythagoras c a b = = = a 2 + b 2 c 2 − b 2 c 2 − a 2 ket : a : sisi alas segitiga b : sisi tegak segitiga c : sisi miring segitiga Suatu segitiga dikatakan siku-siku jika kuadrat dari sisi terpanjangnya ( c ) memiliki nilai yang sama dengan penjumlahan kuadrat sisi-sisi yang lainnya c 2 = a 2 + b 2 Pada △ PQR , Spada QRsehingga PS ⊥ QR . Soal nomor 4a. Perhatikan bahwa △PSQ siku-siku di S dengan sisi terpanjang PQ. Dengan teorema Pythagoras maka panjang PQ yaitu : PQ = = = = = = PS 2 + QS 2 8 2 + 1 6 2 64 + 256 320 64 × 5 8 5 cm Dengan demikian, panjang PQ adalah 8 5 cm. Soal nomor 4b. Perhatikan bahwa △PSR siku-siku di S dengan sisi terpanjang PR. Dengan teorema Pythagoras maka panjang PR yaitu : PR = = = = = = PS 2 + RS 2 8 2 + 4 2 64 + 16 80 15 × 5 4 5 cm Dengan demikian, panjang PR adalah 4 5 cm. Soal nomor 4c. Pada △ PQR , sisi terpanjang adalah QR. Maka diperoleh : QR QR 2 = = = = 4 + 16 20 2 0 2 400 Jumlah kuadrat sisi-sisi lainnya yaitu : PQ 2 + PR 2 = = = ( 320 ) 2 + ( 80 ) 2 320 + 80 400 Dengan demikian, karena QR 2 = PQ 2 + PR 2 maka △ PQR adalah segitiga siku-siku di P .

Ingat!

Rumus Pythagoras

$c a b = = = a^{2} + b^{2} c^{2} - b^{2} c^{2} - a^{2}$

$ket : a : sisi alas segitiga b : sisi tegak segitiga c : sisi miring segitiga$

Suatu segitiga dikatakan siku-siku jika kuadrat dari sisi terpanjangnya $(c)$ memiliki nilai yang sama dengan penjumlahan kuadrat sisi-sisi yang lainnya

$c^{2} = a^{2} + b^{2}$

Pada $△ PQR$ , S pada QR sehingga $PS ⊥ QR$ .

Soal nomor 4a.

Perhatikan bahwa $△PSQ$ siku-siku di S dengan sisi terpanjang PQ. Dengan teorema Pythagoras maka panjang PQ yaitu :

$PQ = = = = = = PS^{2} + QS^{2} 8^{2} + 1 6^{2} 64 + 256 320 64 \times 5 85 cm$

Dengan demikian, panjang $PQ$ adalah $85$ cm.

Soal nomor 4b.

Perhatikan bahwa $△PSR$ siku-siku di S dengan sisi terpanjang PR. Dengan teorema Pythagoras maka panjang $PR$ yaitu :

$PR = = = = = = PS^{2} + RS^{2} 8^{2} + 4^{2} 64 + 16 80 15 \times 5 45 cm$

Dengan demikian, panjang $PR$ adalah $45$ cm.

Soal nomor 4c.

Pada $△ PQR$ , sisi terpanjang adalah QR. Maka diperoleh :

$QR QR^{2} = = = = 4 + 16 20 2 0^{2} 400$

Jumlah kuadrat sisi-sisi lainnya yaitu :

$PQ^{2} + PR^{2} = = = (320)^{2} + (80)^{2} 320 + 80 400$

Dengan demikian, karena $QR^{2} = PQ^{2} + PR^{2}$ maka $△ PQR$ adalah segitiga siku-siku di $P$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.6 (33 rating)

Vheren Chesha Andaresta

Ini yang aku cari!

Muhammad Zuhdy Usman

Pembahasan lengkap banget Mudah dimengerti Ini yang aku cari! Bantu banget

Azkania Fathinah

Pembahasan lengkap banget Bantu banget Makasih ❤️

Helena Jesica Raja

makasih kak Pembahasan lengkap banget

JustAriqah

Pembahasan lengkap banget

Pertanyaan serupa

Gambar di samping menunjukkan persegi PQRS . Panjang sisi-sisi persegi tersebut adalah 8 cm. Buktikan bahwa diagonal PR dan QS saling berpotongan tegak lurus!

4.0

Jawaban terverifikasi

Tentukan panjang hipotenusa pada segitiga berikut!

0.0

Jawaban terverifikasi

Perhatikan △ ABC berikut ini. BD = 4 cm , AD = 8 cm , dan CD = 16 cm . c. Apakah adalah segitiga siku-siku? Jelaskan.

4.8

Jawaban terverifikasi

Mita (M) berada di atas balkon rumahnya. Di kejauhan, ia melihat Katrin (K) yang berjarak 7 m dari bawah balkon tempat Mita berdiri, kemudian ia melihat Lusi (L) yang berada dekat pagar rumah dan berj...

4.8

Jawaban terverifikasi

Pada segitiga ABC terdapat garis tinggi CD. Diketahui panjang AD = 5 2 cm , BD = 10 cm , dan panjang CD = 7 cm . a. Tentukan panjang AC dan BC. b. Apakah segitiga ABC siku siku? Jelaskan.

5.0

Jawaban terverifikasi