Pertanyaan

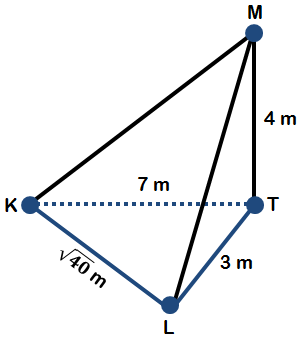
Mita (M) berada di atas balkon rumahnya. Di kejauhan, ia melihat Katrin (K) yang berjarak 7 m dari bawah balkon tempat Mita berdiri, kemudian ia melihat Lusi (L) yang berada dekat pagar rumah dan berjarak 3 m dari tempat yang sama. Tinggi balkon dari permukaan lantai bawah adalah 4 m, dan jarak Katrin dan Lusi adalah 40 m (6,32 m). a. Tunjukkan bahwa △ KLM adalah segitiga siku-siku! b. Sudut manakah yang merupakan sudut siku-siku?

Mita (M) berada di atas balkon rumahnya. Di kejauhan, ia melihat Katrin (K) yang berjarak 7 m dari bawah balkon tempat Mita berdiri, kemudian ia melihat Lusi (L) yang berada dekat pagar rumah dan berjarak 3 m dari tempat yang sama. Tinggi balkon dari permukaan lantai bawah adalah 4 m, dan jarak Katrin dan Lusi adalah $40$ m (6,32 m).

a. Tunjukkan bahwa $△ KLM$ adalah segitiga siku-siku!

b. Sudut manakah yang merupakan sudut siku-siku?

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

E. Lestari

Master Teacher

Mahasiswa/Alumni Universitas Sebelas Maret

Jawaban terverifikasi

Jawaban

karena maka △KLM adalah segitiga siku-siku di L ( ∠ KLM ) .

karena

Error converting from MathML to accessible text.

maka

△KLM

adalah segitiga siku-siku di

L

(∠ KLM)

Pembahasan

Ingat! Rumus Pythagoras c a b = = = a 2 + b 2 c 2 − b 2 c 2 − a 2 ket : a : sisi alas segitiga b : sisi tegak segitiga c : sisi miring segitiga Suatu segitiga dikatakan siku-siku jika kuadrat dari sisi terpanjangnya ( c ) memiliki nilai yang sama dengan penjumlahan kuadrat sisi-sisi yang lainnya c 2 = a 2 + b 2 Perhatikan ilustrasi gambar berikut. Perhatikan △ KTM dengan sisi terpanjang KM . Dengan teorema Pythagoras panjang sisi KM yaitu : KM = = = = = KT 2 + TM 2 7 2 + 4 2 49 + 16 65 8 , 06 m Perhatikan △LTM dengan sisi terpanjang LM . Dengan teorema Pythagoras panjang sisi LM yaitu : LM = = = = = LT 2 + TM 2 3 2 + 4 2 9 + 16 25 5 m Perhatikan △KLM dengan sisi terpanjang KM . KM 2 KM 2 KL 2 + LM 2 KL 2 + LM 2 KL 2 + LM 2 = = = = = ( 65 ) 2 65 ( 40 ) 2 + 5 2 40 + 25 65 Dengan demikian, karena maka △KLM adalah segitiga siku-siku di L ( ∠ KLM ) .

Ingat!

Rumus Pythagoras

$c a b = = = a^{2} + b^{2} c^{2} - b^{2} c^{2} - a^{2}$

$ket : a : sisi alas segitiga b : sisi tegak segitiga c : sisi miring segitiga$

Suatu segitiga dikatakan siku-siku jika kuadrat dari sisi terpanjangnya $(c)$ memiliki nilai yang sama dengan penjumlahan kuadrat sisi-sisi yang lainnya

$c^{2} = a^{2} + b^{2}$

Perhatikan ilustrasi gambar berikut.

Perhatikan $△ KTM$ dengan sisi terpanjang $KM$ . Dengan teorema Pythagoras panjang sisi $KM$ yaitu :

$KM = = = = = KT^{2} + TM^{2} 7^{2} + 4^{2} 49 + 16 65 8, 06 m$

Perhatikan $△LTM$ dengan sisi terpanjang $LM$ . Dengan teorema Pythagoras panjang sisi $LM$ yaitu :

$LM = = = = = LT^{2} + TM^{2} 3^{2} + 4^{2} 9 + 16 25 5 m$

Perhatikan $△KLM$ dengan sisi terpanjang $KM$ .

$KM^{2} KM^{2} KL^{2} + LM^{2} KL^{2} + LM^{2} KL^{2} + LM^{2} = = = = = (65)^{2} 65 (40)^{2} + 5^{2} 40 + 25 65$

Dengan demikian, karena Error converting from MathML to accessible text. maka $△KLM$ adalah segitiga siku-siku di $L$ $(∠ KLM)$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.8 (5 rating)

Latisya Nasywa Khaliza

Bantu banget Makasih ❤️

shelina nayla fadhila

Makasih ❤️

Pertanyaan serupa

II. Untuk soal-soal berikut, kerjakan dengan lengkap! 6. Pada limas T.ABC di atas, panjang BC = 25 cm , AB = 24 cm , dan TC = 51 cm . a. Hitunglah panjang AC, AT, dan BT! b. Tunjukkan...

4.6

Jawaban terverifikasi

II. Untuk soal-soal berikut, kerjakan dengan lengkap! 6. Pada limas T.ABC di atas, panjang BC = 25 cm , AB = 24 cm , dan TC = 51 cm . a. Hitunglah panjang AC, AT, dan BT! b. Tunjukkan...

4.6

Jawaban terverifikasi

Perhatikan limas T.ABCDdi bawah. Alas limas berbentuk persegi dengan panjang sisi 48 cm dan panjang TO = 32 cm . Panjang TE adalah ...

4.5

Jawaban terverifikasi

Pada kubus ABCD.EFGH di atas, panjang rusuk AB = 12 cm . Hitunglah: b. luas △ BCH

4.8

Jawaban terverifikasi

Diketahui sebuah balok denganpanjang = 15 cm dan lebar = 10 cm. Panjang diagonal sisinya adalah ... cm

5.0

Jawaban terverifikasi