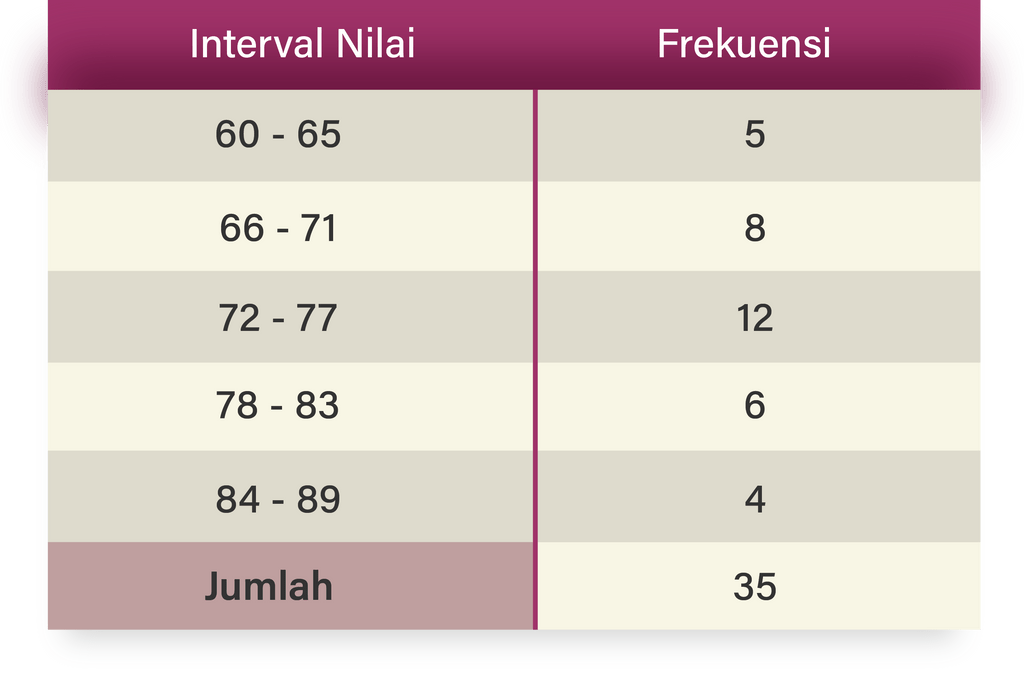
-Menentukan mean, ingat kembali konsep mean dengan menggunakan nilai tengah:
x=i=1∑k fii=1∑k xi⋅fi
dimana fi frekuensi ke-i, dan xi nilai tengah kelas ke-i.
Nilai tengah dapat diperoleh dengan cara:
x1x2x3x4x5=====260+65=62,5266+71=68,5272+77=74,5278+83=80,5284+89=86,5
kemudian
∑i=15xi⋅fi===(62,5)⋅5+(68,5)⋅8+(74,5)⋅12+(80,5)⋅6+(86,5)⋅4312,5+548+894+483+3462.583,5
sehingga mean dari data tersebut adalah
x===i=1∑5 fii=1∑5 xi⋅fi352.583,573,8
-Menentukan median
Me=Tb+(fi2n−fk)⋅p
Dimana Tb tepi bawah kelas median,  panjang kelas interval, n total frekuensi, fk jumlah frekuensi sebelum kelas median, fi kelas median. Maka dari data tersebut diperoleh:
panjang kelas interval, n total frekuensi, fk jumlah frekuensi sebelum kelas median, fi kelas median. Maka dari data tersebut diperoleh:
2nfifkpTb========235=17,5125+81377−72+1672−0,571,5
Sehingga
Me======Tb+(fi2n−fk)⋅p71,5+(1217,5−13)⋅671,5+(124,5)⋅571,5+1222,571,5+1,87573,4
-Menentukan modus
Mo=Tb+(d1+d2d1)⋅p
Dimana Tb tepi bawah kelas modus, d1 selisih frekuensi kelas modus dengan frekuensi kelas modus sebelumnya, d2 selisih frekuensi kelas modus dengan frekuensi kelas modus sesudahnya, dan  panjang kelas interval. Dari data tersebut frekuensi paling besar adalah 12 maka kelas modus adalah 12 sehingga:
panjang kelas interval. Dari data tersebut frekuensi paling besar adalah 12 maka kelas modus adalah 12 sehingga:
Tbd1d2p========72−0,571,512−8412−6677−72+16
Sehingga
Mo======Tb+(d1+d2d1)⋅p71,5+(4+64)⋅671,5+(104)⋅671,5+102471,5+2,473,9
Dengan demikian mean, median, dan modus dari data tersebut berturut-turut adalah 73,8, 73,4, dan 73,9.