Pertanyaan

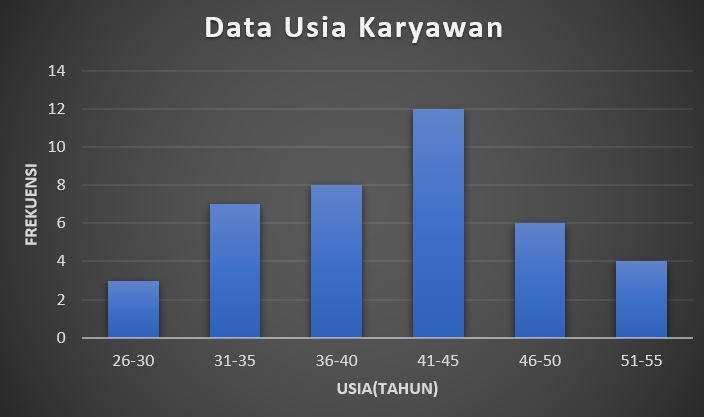
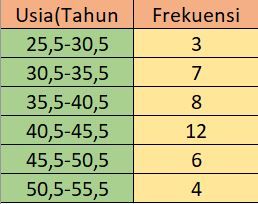
Tabel berikut menunjukkan data usia karyawan di suatu perusahaan: Berdasarkan tabel distribusi frekuensi diatas tentukanlah: a. Nilai Mean (rataannya) b. Nilai Median c. Gambarlah tabel distribusi frekuensi tersebut kedalam diagram batang d. Tentukan nilai tepi bawah dan tepi atasnya e. Tentukan batas bawah dan batas atasnya f. Nilai Modusnya

Tabel berikut menunjukkan data usia karyawan di suatu perusahaan:

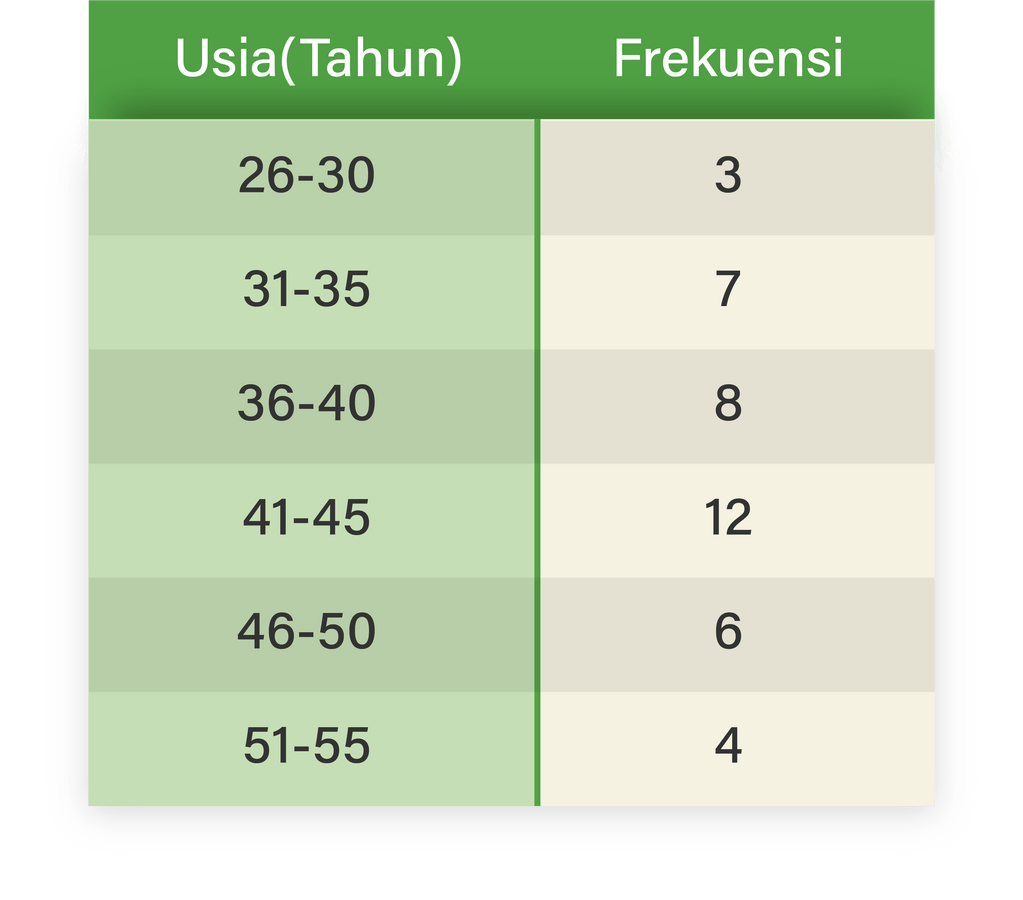
Berdasarkan tabel distribusi frekuensi diatas tentukanlah:
a. Nilai Mean (rataannya)
b. Nilai Median
c. Gambarlah tabel distribusi frekuensi tersebut kedalam diagram batang
d. Tentukan nilai tepi bawah dan tepi atasnya
e. Tentukan batas bawah dan batas atasnya
f. Nilai Modusnya

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Y. Umi

Master Teacher

Mahasiswa/Alumni Universitas Gadjah Mada

Jawaban terverifikasi

Jawaban

nilai modusnya adalah 42 , 5 .

nilai modusnya adalah

42, 5

Pembahasan

Tabel berikut menunjukkan data usia karyawan di suatu perusahaan: Berdasarkan tabel distribusi frekuensi diatas akan dicari a. Nilai Mean (rataannya) Nilai tengah adalah pemusatan data yang membagi suatu data menjadi setengah (50%) data terkecil dan terbesarnya. Untuk mencari mean diperlukan nilai tengai tengah dari setiap interval. Mlsalkan x = = = = = x = 1 ∑ f i 5 x = 1 ∑ x i f i 5 3 + 7 + 8 + 12 + 6 28 ⋅ 3 + 33 ⋅ 7 + 38 ⋅ 8 + 43 ⋅ 12 + 48 ⋅ 6 3 + 7 + 8 + 12 + 6 84 + 231 + 304 + 516 + 288 36 1.423 39 , 53 Dengan demikian, nilai meandari data di atas adalah 39 , 53 . b. Nilai Median median adalah data titik tengah Me = t b + ⎝ ⎛ F m 2 n − F ⎠ ⎞ p dengan t b adalah tepi bawah dari kelas median F adalah frekuensi kumulatif sebelum kelas median F m adalah frekuensi kelas median adalah interval sehingga Me = = = = = t b + ⎝ ⎛ F m 2 n − F ⎠ ⎞ p 35 , 5 + ⎝ ⎛ 8 2 36 − 10 ⎠ ⎞ 5 35 , 5 + ( 8 18 − 10 ) 5 35 , 5 + 5 40 , 5 Dengan demikian, median dari data di atas adalah 40 , 5 . c. Gambar tabel distribusi frekuensi dalam diagram batang d. Tentukan nilai tepi bawah dan tepi atasnya Untuk mencari tepi kelas dapat dipakai rumus berikut ini. Tepi bawah Tepi atas = = batas bawah –0 , 5 batas atas + 0 , 5 e. Tentukan batas bawah dan batas atasnya Berdasarkan tabel distribusi frekuensi di atas, angka 26 , 31 , 36 , 41 , 46 , 51 merupakan batas bawah dari tiap-tiap kelas, sedangkan angka 30 , 35 , 40 , 45 , 50 , 55 merupakan batas atas dari tiap-tiap kelas. f. Nilai Modusnya Modus adalah salah satu cara mengalisis dari berdasarkan frekuensi kemunculan suatu nilai. Mo = t b + ( d 1 + d 2 d 1 ) p dengan t b adalah tepi bawah dari kelas median d 1 adalah selisih frekuensi kelas modus dengan frekuensi sebelum kelas modus d 2 adalah selisih frekuensi kelas modus dengan frekuensi setelah kelas modus adalah interval sehingga Mo = = = = = t b + ( d 1 + d 2 d 1 ) p 40 , 5 + ( 4 + 6 4 ) 5 40 , 5 + ( 10 4 ) 5 40 , 5 + 2 42 , 5 Dengan demikian, nilai modusnya adalah 42 , 5 .

Tabel berikut menunjukkan data usia karyawan di suatu perusahaan:

Berdasarkan tabel distribusi frekuensi diatas akan dicari
a. Nilai Mean (rataannya)

Nilai tengah adalah pemusatan data yang membagi suatu data menjadi setengah (50%) data terkecil dan terbesarnya. Untuk mencari mean diperlukan nilai tengai tengah dari setiap interval. Mlsalkan

$\overline{x} = = = = = \frac{x = 1 \sum x _{i} f _{i} 5}{x = 1 \sum f _{i} 5} \frac{28 \cdot 3 + 33 \cdot 7 + 38 \cdot 8 + 43 \cdot 12 + 48 \cdot 6}{3 + 7 + 8 + 12 + 6} \frac{84 + 231 + 304 + 516 + 288}{3 + 7 + 8 + 12 + 6} \frac{1.423}{36} 39, 53$

Dengan demikian, nilai mean dari data di atas adalah $39, 53$ .
b. Nilai Median

median adalah data titik tengah

$Me = t_{b} + ⎝ ⎛ \frac{\frac{n}{2} - F}{F _{m}} ⎠ ⎞ p$

dengan

$t_{b}$ adalah tepi bawah dari kelas median

$F$ adalah frekuensi kumulatif sebelum kelas median

$F_{m}$ adalah frekuensi kelas median

$p$ adalah interval

sehingga

$Me = = = = = t_{b} + ⎝ ⎛ \frac{\frac{n}{2} - F}{F _{m}} ⎠ ⎞ p 35, 5 + ⎝ ⎛ \frac{\frac{36}{2} - 10}{8} ⎠ ⎞ 5 35, 5 + (\frac{18 - 10}{8}) 5 35, 5 + 5 40, 5$

Dengan demikian, median dari data di atas adalah $40, 5$ .

c. Gambar tabel distribusi frekuensi dalam diagram batang

d. Tentukan nilai tepi bawah dan tepi atasnya

Untuk mencari tepi kelas dapat dipakai rumus berikut ini.

$Tepi bawah Tepi atas = = batas bawah -0, 5 batas atas + 0, 5$

e. Tentukan batas bawah dan batas atasnya

Berdasarkan tabel distribusi frekuensi di atas, angka $26, 31, 36, 41, 46, 51$ merupakan batas bawah dari tiap-tiap kelas, sedangkan angka $30, 35, 40, 45, 50, 55$ merupakan batas atas dari tiap-tiap kelas.

f. Nilai Modusnya

Modus adalah salah satu cara mengalisis dari berdasarkan frekuensi kemunculan suatu nilai.

$Mo = t_{b} + (\frac{d _{1}}{d _{1} + d _{2}}) p$

dengan

$t_{b}$ adalah tepi bawah dari kelas median

$d_{1}$ adalah selisih frekuensi kelas modus dengan frekuensi sebelum kelas modus

$d_{2}$ adalah selisih frekuensi kelas modus dengan frekuensi setelah kelas modus

$p$ adalah interval

sehingga

$Mo = = = = = t_{b} + (\frac{d _{1}}{d _{1} + d _{2}}) p 40, 5 + (\frac{4}{4 + 6}) 5 40, 5 + (\frac{4}{10}) 5 40, 5 + 2 42, 5$

Dengan demikian, nilai modusnya adalah $42, 5$ .

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.6 (3 rating)

Hiping Marta

Makasih ❤️

Pertanyaan serupa

Diketahui data: 38 42 42 40 32 38 45 45 35 38 39 48 42 41 52 30 40 43 31 30 43 43 41 50 41 41 41 39 54 31 42 41 35 36 43 49 33 37 36 49 a. Buatlah distribusi frekuensi data berkelomp...

0.0

Jawaban terverifikasi

Jika titik-titik tengah kelas interval dari distribusi frekuensi sekumpulan barang tercatat besarnya 225 g r , 234 g r , 243 g , 252 g r , 261 g r , 270 g r , dan 279 g r , tentukan: a. panjang kelas...

5.0

Jawaban terverifikasi

Diketahui data nilai ulangan dari 30 siswa sebagai berikut. Berdasarkan tabel di samping, tentukan : a. Banyak kelas b. Batas atas kelas kedua c. Batas bawah kelas keempat d. Tepi atas kelas...

3.7

Jawaban terverifikasi

Diketahui data: 38 42 42 40 32 38 45 45 35 38 39 48 42 41 52 30 40 43 31 30 43 43 41 50 41 41 41 39 54 31 42 41 35 36 43 49 33 37 36 49 a. Buatlah distribusi frekuensi data berkelomp...

0.0

Jawaban terverifikasi

Diketahui data nilai ulangan dari 30 siswa sebagai berikut. Berdasarkan tabel di samping, tentukan : a. Banyak kelas b. Batas atas kelas kedua c. Batas bawah kelas keempat d. Tepi atas kelas...

3.7

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS