Iklan
Pertanyaan
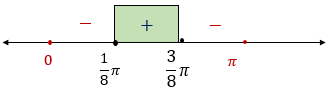
Pada interval 0 ≤ x ≤ π pertidaksamaan 1 − 2 sin 2 x ≤ 0 benar untuk ....
Pada interval pertidaksamaan benar untuk ....
Iklan
NP
N. Puspita
Master Teacher
Jawaban terverifikasi
2
5.0 (6 rating)
Iklan
Pertanyaan serupa
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia