Pada gambar berikut, berapakah nilai dari x ?

Pembahasan

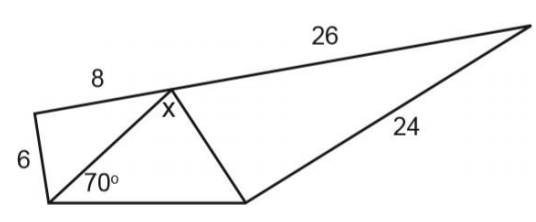
Tripel Pythagoras adalah tripel bilangan bulat positif , b , dan yang memenuhi a 2 + b 2 = c 2 dengan merupakan sisi miring (sisi terpanjang) pada segitiga siku-siku. Tripel Pythagoras yang paling sederhana adalah 3 , 4 , 5 atau 5 , 12 , 13 . Jika , b , dan merupakan tripel Pythagoras dan k suatu bilangan bulat positif, maka ka , kb , dan k c juga merupakan tripel Pythagoras. Pada gambar di atas, panjang sisi-sisi segitiga sebelah kiri membentuk tripel Pythagoras dengan perbandingan 6 ÷ 8 ÷ 10 yang merupakan kelipatan dari tripel Pythagoras 3 ÷ 4 ÷ 5 .Dengan demikian, diperoleh panjang sisi segitiga sebelah kiri yang belum diketahui, yaitu 10 . Pada segitiga sebelah kanan, perbandingan panjang sisi-sisinyamembentuk tripel Pythagoras dengan perbandingan 10 ÷ 12 ÷ 13 yang merupakan kelipatan dari tripel Pythagoras 5 ÷ 12 ÷ 13 .Dengan demikian, diperoleh panjang sisi segitiga sebelah kananyang belum diketahui, yaitu 10 . Dari uraian di atas, dapat diketahui bahwa segitiga yang berada di tengah merupakan segitiga sama kaki. Pada sebarang segitiga, sisi yang sama berarti sudut yang berseberangan dengan sisi tersebut juga sama besar sehingga besar sudut yang di dekat sudut 7 0 ∘ juga sebesar 7 0 ∘ . Apabila jumlah sudut dalam segitiga adalah 18 0 ∘ , maka nilai x dapat ditentukan sebagai berikut. 7 0 ∘ + 7 0 ∘ + x 14 0 ∘ + x x ​ = = = ​ 18 0 ∘ 18 0 ∘ 4 0 ∘ ​ Oleh karena itu, jawaban yang tepat adalah A.