Pertanyaan

Soal no 3.

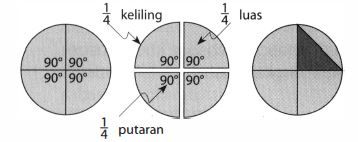
Untuk membagi lingkaran sama besar, paling mudah dengan membagi melalui pusat lingkaran. Jika lingkaran belum dipotong, maka besar sudut adalah 1 putaran atau $360^\circ$ . Jika lingkaran ingin dibagi menjadi empat bagian sama besar, maka sudut pusat lingkaran tersebut dibagi empat, masing-masing sebesar $90^\circ$ .

Tentukan keliling lingkaran (bagian yang melengkung saja) dari setiap potongan.
Tentukan luas setiap juring (sektor).
Tentukan luas segitiga yang diarsir lebih gelap.
Tentukan keliling segitiga.
Bandingkan ukuran keliling lingkaran dengan panjang sisi miring segitiga.

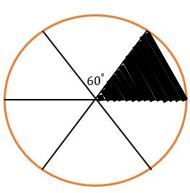
Kerjakan sekali lagi soal nomor 3, jika lingkaran dibagi menjadi enam bagian.

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah π : 3 .

perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah

π : 3

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah a. 3 1 π r b. 6 1 π r 2 c. 4 r 2 3 d. 3 r e. π : 3 Ingat! Keliling adalah sebuah lingkaran membentuk garis lengkung dengan panjang tertentu. Rumus menghitung keliling lingkaran apabila jari-jarinya diketahui adalah: K = 2 × π × r Rumus untuk menghitung luas lingkaran adalah: L = π × r 2 Rumus untuk menghitung luas segitiga adalah: L = 2 1 × a × t dengan a = alas , t = tinggi . Rumus pythagoras dalam segitiga adalah: c 2 c = = a 2 + b 2 a 2 + b 2 dengan c = sisi miring segitiga Rumus untuk menghitung keliling segitiga adalah: K = = jumlah semua sisi segitiga a + b + c Perhatikan ilustrasi berikut! a.Berdasarkan rumus keliling lingkaran, maka dapat dihitung rumus keliling seperenamlingkaran (bagian yang melengkung saja) sebagai berikut: K = = 6 1 × 2 × π × r 3 1 × π × r Dengan demikian, keliling seperenamlingkaran (bagian yang melengkung saja) dari setiap potongan adalah 3 1 π r . b.Berdasarkan rumus menghitung luas lingkaran, maka dapat dihitung luas setiap juring yang berbentuk seperenamlingkaran sebagai berikut: L = 6 1 × π × r 2 Dengan demikian, luas setiap juring yang berbentuk seperenamlingkaran adalah 6 1 π r 2 . c. Perhatikan bahwa segitiga yang terbentuk adalah segitiga sama sisi karena semua sudutnya adalah 6 0 ∘ .Pertama kita cari tinggi segitiga tersebut dengan Pythagoras: t = = = = r 2 − ( 2 1 r ) 2 r 2 − 4 1 r 2 4 3 r 2 2 1 r 3 Maka luas segitiganya adalah: L = 2 1 × a × t = 2 1 × r × 2 1 r 3 = 4 r 2 3 Dengan demikian, luas segitiga yang diarsir lebih gelapadalah 4 r 2 3 . d.Perhatikan bahwa segitiga yang terbentuk adalah segitiga sama sisi karena semua sudutnya adalah 6 0 ∘ . Maka semua sisinya mempunyai panjang r .Jadi, keliling lingkaran dengan a = t = sisi miring = r adalah: K = = = jumlah semua sisi segitiga r + r + r 3 r Dengan demikian, keliling segitiga adalah 3 r . e. Perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah: K : sisi miring lingkaran = = = 3 1 π r : r 3 1 π : 1 π : 3 Dengan demikian,perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah π : 3 .

Jawaban yang benar untuk pertanyaan tersebut adalah

a. $\frac{1}{3} π r$

b. $\frac{1}{6} π r^{2}$

c. $\frac{r ^{2}}{4} 3$

d. $3 r$

e. $π : 3$

Ingat!

Keliling adalah sebuah lingkaran membentuk garis lengkung dengan panjang tertentu.
Rumus menghitung keliling lingkaran apabila jari-jarinya diketahui adalah:

$K = 2 \times π \times r$

Rumus untuk menghitung luas lingkaran adalah:

$L = π \times r^{2}$

Rumus untuk menghitung luas segitiga adalah:

$L = \frac{1}{2} \times a \times t$

dengan $a = alas, t = tinggi$ .

Rumus pythagoras dalam segitiga adalah:

$c^{2} c = = a^{2} + b^{2} a^{2} + b^{2}$

dengan $c = sisi miring segitiga$

Rumus untuk menghitung keliling segitiga adalah:

$K = = jumlah semua sisi segitiga a + b + c$

Perhatikan ilustrasi berikut!

a. Berdasarkan rumus keliling lingkaran, maka dapat dihitung rumus keliling seperenam lingkaran (bagian yang melengkung saja) sebagai berikut:

$K = = \frac{1}{6} \times 2 \times π \times r \frac{1}{3} \times π \times r$

Dengan demikian, keliling seperenam lingkaran (bagian yang melengkung saja) dari setiap potongan adalah $\frac{1}{3} π r$ .

b. Berdasarkan rumus menghitung luas lingkaran, maka dapat dihitung luas setiap juring yang berbentuk seperenam lingkaran sebagai berikut:

$L = \frac{1}{6} \times π \times r^{2}$

Dengan demikian, luas setiap juring yang berbentuk seperenam lingkaran adalah $\frac{1}{6} π r^{2}$ .

c. Perhatikan bahwa segitiga yang terbentuk adalah segitiga sama sisi karena semua sudutnya adalah $6 0^{\circ}$ . Pertama kita cari tinggi segitiga tersebut dengan Pythagoras:

$t = = = = r^{2} - (\frac{1}{2} r)^{2} r^{2} - \frac{1}{4} r^{2} \frac{3}{4} r^{2} \frac{1}{2} r 3$

Maka luas segitiganya adalah:

$L = \frac{1}{2} \times a \times t = \frac{1}{2} \times r \times \frac{1}{2} r 3 = \frac{r ^{2}}{4} 3$

Dengan demikian, luas segitiga yang diarsir lebih gelap adalah $\frac{r ^{2}}{4} 3$ .

d. Perhatikan bahwa segitiga yang terbentuk adalah segitiga sama sisi karena semua sudutnya adalah $6 0^{\circ}$ . Maka semua sisinya mempunyai panjang $r$ . Jadi, keliling lingkaran dengan $a = t = sisi miring = r$ adalah:

$K = = = jumlah semua sisi segitiga r + r + r 3 r$

Dengan demikian, keliling segitiga adalah $3 r$ .

e. Perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah:

$K : sisi miring lingkaran = = = \frac{1}{3} π r : r \frac{1}{3} π : 1 π : 3$

Dengan demikian, perbandingan ukuran keliling lingkaran dengan panjang sisi miring segitiga adalah $π : 3$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.0 (4 rating)

Casidi Sidi

Bantu banget Makasih ❤️

HENDRIKUS JEMAT

Pembahasan lengkap banget Ini yang aku cari! Mudah dimengerti Bantu banget Makasih ❤️

Pertanyaan serupa

Perhatikan gambar berikut. Jika O merupakan titik pusat lingkaran dan π = 7 22 , tentukan: a. luas lingkaran; b. keliling lingkaran c. luas juring mayor OAB dan d. panjang busur ma...

3.6

Jawaban terverifikasi

Diketahui panjang jari-jari suatu lingkaran adalah 21 cm dan panjang busurnya 22 cm .Luas juring lingkaran tersebut adalah ....

4.3

Jawaban terverifikasi

Perhatikan gambar berikut. Jika O merupakan titik pusat lingkaran dan π = 7 22 , tentukan: a. luas lingkaran; b. keliling lingkaran c. luas juring mayor OAB dan d. panjang busur ma...

3.6

Jawaban terverifikasi

Kerjakan sekali lagi soal nomor 3 , jika lingkaran dibagi menjadi delapan bagian. Bandingkan hasilnya dengan lingkaran yang dibagi menjadi empat bagian.

5.0

Jawaban terverifikasi

Hitunglah panjang busur dan luas juring dari lingkaran berikut.

4.5

Jawaban terverifikasi