Iklan
Pertanyaan
Soal no 3.
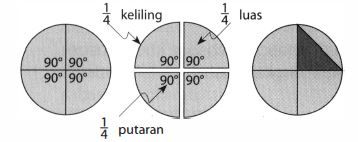
Untuk membagi lingkaran sama besar, paling mudah dengan membagi melalui pusat lingkaran. Jika lingkaran belum dipotong, maka besar sudut adalah 1 putaran atau . Jika lingkaran ingin dibagi menjadi empat bagian sama besar, maka sudut pusat lingkaran tersebut dibagi empat, masing-masing sebesar
.
- Tentukan keliling lingkaran (bagian yang melengkung saja) dari setiap potongan.
- Tentukan luas setiap juring (sektor).
- Tentukan luas segitiga yang diarsir lebih gelap.
- Tentukan keliling segitiga.
- Bandingkan ukuran keliling lingkaran dengan panjang sisi miring segitiga.
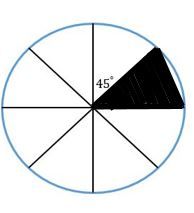
Kerjakan sekali lagi soal nomor 3 , jika lingkaran dibagi menjadi delapan bagian. Bandingkan hasilnya dengan lingkaran yang dibagi menjadi empat bagian.
Kerjakan sekali lagi soal nomor , jika lingkaran dibagi menjadi delapan bagian. Bandingkan hasilnya dengan lingkaran yang dibagi menjadi empat bagian.
Iklan
A. Salim
Master Teacher
Mahasiswa/Alumni Universitas Pelita Harapan
5
5.0 (2 rating)
Sus aandarwati
Bantu banget Ini yang aku cari! Pembahasan lengkap banget Mudah dimengerti Makasih ❤️
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia