Dengan menggunakan sifat bilangan berpangkat berikut.
-

-

pertidaksamaan  dapat diuraikan menjadi sebagai berikut.
dapat diuraikan menjadi sebagai berikut.

Misal,  maka diperoleh:
maka diperoleh:

Kemudian, nilai  yang memenuhi pertidaksamaan di atas sebagai berikut.
yang memenuhi pertidaksamaan di atas sebagai berikut.
- Nilai
 saat sama dengan
saat sama dengan 

 atau
atau 
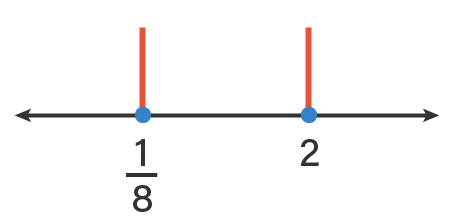
Berdasarkan garis bilangan di atas, terdapat  interval yaitu
interval yaitu  ,
,  , dan
, dan  . Uji titik pada setiap interval tersebut sebagai berikut.
. Uji titik pada setiap interval tersebut sebagai berikut.
- Ketika
 , pilih
, pilih  maka diperoleh:
maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  positif atau lebih dari
positif atau lebih dari  .
.
- Ketika
 , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  negatif atau kurang dari
negatif atau kurang dari  .
.
- Ketika
 , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  positif atau lebih dari
positif atau lebih dari  .
.
Hasil di atas dapat dituliskan pada garis bilangan sebagai berikut.
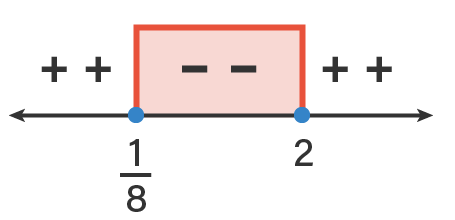
Berdasarkan garis bilangan di atas, interval nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  adalah
adalah  , maka nilai
, maka nilai  yang memenuhi sebagai berikut.
yang memenuhi sebagai berikut.

 dan
dan 
Dengan menggunakan sifat bilangan berpangkat  , maka diperoleh:
, maka diperoleh:
 dan
dan 
Kemudian, ingat bahwa untuk  , jika
, jika  , maka
, maka  dan jika
dan jika  , maka
, maka  , sehingga diperoleh:
, sehingga diperoleh:
 dan
dan 

Nilai  yang memenuhi yaitu
yang memenuhi yaitu  , maka himpunan penyelesaian dari pertidaksamaan
, maka himpunan penyelesaian dari pertidaksamaan  adalah
adalah  .
.
Oleh karena itu, jawaban yang benar adalah E.



















