Diketahui pertidaksamaan  . Dengan menggunakan sifat bentuk logaritma berikut.
. Dengan menggunakan sifat bentuk logaritma berikut.
untuk  dan
dan  , berlaku:
, berlaku:

-


maka diperoleh:

Kemudian, ingat bahwa, jika  ,
,  dan
dan  maka
maka  dan
dan  .
.
Misal,  maka dari pertidaksamaan
maka dari pertidaksamaan  diperoleh:
diperoleh:

Nilai  yang memenuhi saat sama dengan
yang memenuhi saat sama dengan  sebagai berikut.
sebagai berikut.

Lalu, nilai  di atas dapat dituliskan pada garis bilangan sebagai berikut.
di atas dapat dituliskan pada garis bilangan sebagai berikut.
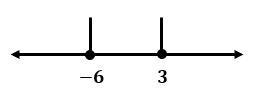
Berdasarkan garis bilangan di atas, terdapat  daerah yaitu
daerah yaitu  ,
,  , dan
, dan  . Uji titik pada setiap daerah tersebut sebagai berikut.
. Uji titik pada setiap daerah tersebut sebagai berikut.
Ketika  , pilih
, pilih  maka diperoleh:
maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  lebih dari
lebih dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  kurang dari
kurang dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  lebih dari
lebih dari  .
.
Hasil di atas dapat dituliskan pada garis bilangan sebagai berikut.
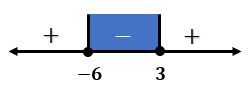
Berdasarkan garis bilangan di atas, nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  adalah
adalah  .
.

Nilai  yang memenuhi saat sama dengan
yang memenuhi saat sama dengan  sebagai berikut.
sebagai berikut.

Lalu, nilai  di atas dapat dituliskan pada garis bilangan sebagai berikut.
di atas dapat dituliskan pada garis bilangan sebagai berikut.
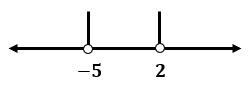
Berdasarkan garis bilangan di atas, terdapat  daerah yaitu
daerah yaitu  ,
,  , dan
, dan  . Uji titik pada setiap daerah tersebut sebagai berikut.
. Uji titik pada setiap daerah tersebut sebagai berikut.
Ketika  , pilih
, pilih  maka diperoleh:
maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  lebih dari
lebih dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  kurang dari
kurang dari  .
.
Ketika  , pilih
, pilih  , maka diperoleh:
, maka diperoleh:


Berdasarkan uji titik di atas, ketika  , nilai
, nilai  lebih dari
lebih dari  .
.
Hasil di atas dapat dituliskan pada garis bilangan sebagai berikut.
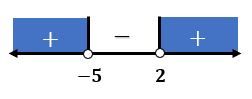
Berdasarkan garis bilangan di atas, nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  adalah
adalah  atau
atau  .
.
Kemudian, numerus dari suatu bentuk logaritma bernilai lebih dari  , maka dari
, maka dari  terdapat syarat
terdapat syarat  dan
dan  . Jika
. Jika  , maka
, maka  dan jika
dan jika  , maka
, maka  .
.
Lalu, penyelesaian dari  adalah irisan dari penyelesaian
adalah irisan dari penyelesaian  ,
,  ,
,  , dan
, dan  . Irisan dari keempat penyelesaian tersebut dapat ditentukan dengan garis bilangan sebagai berikut.
. Irisan dari keempat penyelesaian tersebut dapat ditentukan dengan garis bilangan sebagai berikut.
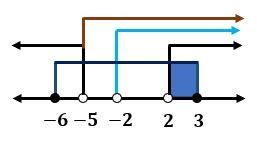
Berdasarkan garis bilangan di atas, himpunan penyelesaian pertidaksamaan  adalah
adalah  .
.
Oleh karena itu, jawaban yang benar adalah D.




















