Diketahui  . Basis dari logaritma pada pertidaksamaan tersebut adalah
. Basis dari logaritma pada pertidaksamaan tersebut adalah  ,
,  maka:
maka:

 apabila
apabila  dan
dan  atau
atau  dan
dan  . Saat
. Saat  dan
dan  , nilai
, nilai  yang memenuhi sebagai berikut.
yang memenuhi sebagai berikut.


 dan
dan  maka nilai
maka nilai  yang memenuhi keduanya yaitu
yang memenuhi keduanya yaitu  . Garis bilangannya sebagai berikut.
. Garis bilangannya sebagai berikut.
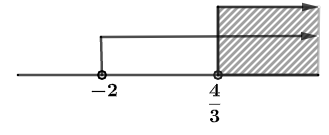
Saat  dan
dan  , nilai
, nilai  yang memenuhi sebagai berikut.
yang memenuhi sebagai berikut.


 dan
dan  maka nilai
maka nilai  yang memenuhi keduanya yaitu
yang memenuhi keduanya yaitu  . Garis bilangannya sebagai berikut.
. Garis bilangannya sebagai berikut.
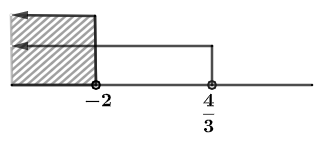
Berdasarkan uraian di atas maka nilai  yang memenuhi
yang memenuhi  yaitu
yaitu  atau
atau  .
.
Kemudian, numerus harus lebih dari sama dengan  maka
maka  dan
dan  . Nilai
. Nilai  yang memenuhi
yang memenuhi  sebagai berikut.
sebagai berikut.

 apabila
apabila  dan
dan  atau
atau  dan
dan  . Saat
. Saat  dan
dan  , nilai
, nilai  yang memenuhi sebagai berikut.
yang memenuhi sebagai berikut.

 dan
dan  maka nilai
maka nilai  yang memenuhi keduanya yaitu
yang memenuhi keduanya yaitu  . Garis bilangannya sebagai berikut.
. Garis bilangannya sebagai berikut.
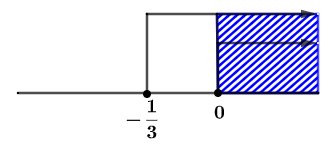
Saat  dan
dan  , nilai
, nilai  yang memenuhi sebagai berikut.
yang memenuhi sebagai berikut.

 dan
dan  maka nilai
maka nilai  yang memenuhi keduanya yaitu
yang memenuhi keduanya yaitu  . Garis bilangannya sebagai berikut.
. Garis bilangannya sebagai berikut.
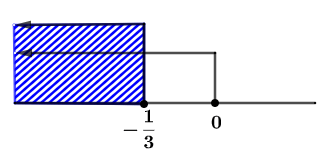
Berdasarkan uraian di atas maka nilai  yang memenuhi
yang memenuhi  yaitu
yaitu  atau
atau  .
.
Selanjutnya, nilai  yang memenuhi
yang memenuhi  sebagai berikut.
sebagai berikut.

Irisan dari nilai  yang memenuhi
yang memenuhi  ,
,  , dan
, dan  adalah nilai
adalah nilai  yang memenuhi pertidaksamaan
yang memenuhi pertidaksamaan  . Irisan nilai
. Irisan nilai  yang memenuhi tersebut sebagai berikut.
yang memenuhi tersebut sebagai berikut.
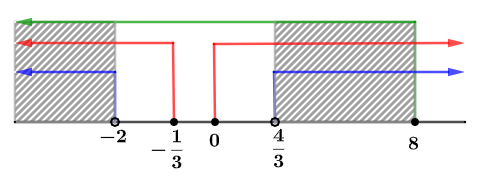
Berdasarkan garis bilangan di atas, nilai  yang memenuhi yaitu
yang memenuhi yaitu  atau
atau  .
.
Dengan demikian, Himpunan penyelesaian dari pertidaksamaan logaritma  adalah
adalah  .
.




















