Diketahui sistem pertidaksamaan  .
.
Daerah penyelesaian sistem pertidaksamaan tersebut dapat ditentukan dengan menentukan daerah penyelesaian dari setiap pertidaksamaan. Daerah penyelesaian dari setiap pertidaksamaan tersebut sebagai berikut.
Daerah penyelesaian pertidaksamaan 
Langkah pertama untuk menentukan daerah penyelesaian pertidaksamaan  adalah dengan melukis kurva pembatas
adalah dengan melukis kurva pembatas  . Kurva
. Kurva  berbentuk parabola terbuka ke atas (koefisien
berbentuk parabola terbuka ke atas (koefisien  positif) dengan titik-titik sebagai berikut.
positif) dengan titik-titik sebagai berikut.


Selain dengan menggunakan rumus di atas, nilai  dapat ditentukan dengan mensubstitusikan
dapat ditentukan dengan mensubstitusikan  pada persamaan
pada persamaan  . Titik balik kurva
. Titik balik kurva  adalah
adalah  .
.
- Titik potong sumbu
 dan sumbu
dan sumbu 
Titik belok  adalah
adalah  , maka kurva memotong sumbu
, maka kurva memotong sumbu  di titik
di titik  . Selanjutnya titik potong kurva
. Selanjutnya titik potong kurva  pada sumbu
pada sumbu  (saat
(saat  ) sebagai berikut.
) sebagai berikut.

 atau
atau 
Titik potong kurva  pada sumbu
pada sumbu  adalah
adalah  dan
dan  .
.
Berdasarkan titik balik dan titik potong di atas, dapat dilukis kurva  dengan menghubungkan titik-titik tersebut. Kurva
dengan menghubungkan titik-titik tersebut. Kurva  dilukis dengan garis penuh karena tanda pertidaksamaannya kurang dari sama dengan.
dilukis dengan garis penuh karena tanda pertidaksamaannya kurang dari sama dengan.
Selanjutnya adalah menentukan daerah penyelesaian. Daerah penyelesaian pertidaksamaan  , dapat ditentukan dengan melakukan uji titik di dalam atau diluar kurva
, dapat ditentukan dengan melakukan uji titik di dalam atau diluar kurva  . Misal, pilih titik
. Misal, pilih titik  di dalam kurva
di dalam kurva  , maka diperoleh:
, maka diperoleh:


Titik  tidak memenuhi pertidaksamaan
tidak memenuhi pertidaksamaan  , maka daerah penyelesaian dari
, maka daerah penyelesaian dari  , berada di luar kurva
, berada di luar kurva  .
.
Daerah penyelesaian pertidaksamaan 
Langkah pertama untuk menentukan daerah penyelesaian pertidaksamaan  adalah dengan melukis garis pembatas
adalah dengan melukis garis pembatas  . Titik potong garis
. Titik potong garis  terhadap sumbu
terhadap sumbu  dan sumbu
dan sumbu  sebagai berikut.
sebagai berikut.
Titik potong sumbu 

Titik potong garis  pada sumbu
pada sumbu  adalah
adalah  .
.
Titik potong sumbu 

Titik potong garis  pada sumbu
pada sumbu  adalah
adalah  .
.
Dengan menggunakan titik potong di atas, dapat dilukis garis lurus  dengan menghubungkan kedua titik tersebut. Kurva
dengan menghubungkan kedua titik tersebut. Kurva  dilukis dengan garis putus-putus karena tanda pertidaksamaannya kurang dari.
dilukis dengan garis putus-putus karena tanda pertidaksamaannya kurang dari.
Selanjutnya adalah menentukan daerah penyelesaian. Daerah penyelesaian pertidaksamaan  , dapat ditentukan dengan melakukan uji titik di atas atau dibawah garis
, dapat ditentukan dengan melakukan uji titik di atas atau dibawah garis  . Misal, pilih titik
. Misal, pilih titik  di atas garis
di atas garis  , maka diperoleh:
, maka diperoleh:


Titik  memenuhi pertidaksamaan
memenuhi pertidaksamaan  , maka daerah penyelesaian dari
, maka daerah penyelesaian dari  , berada di atas garis
, berada di atas garis  .
.
Kemudian, daerah penyelesaian sistem pertidaksamaan  adalah irisan daerah penyelesaian pertidaksamaan
adalah irisan daerah penyelesaian pertidaksamaan  dan
dan  . Gambar grafik daerah penyelesaian pertidaksamaan tersebut sebagai berikut.
. Gambar grafik daerah penyelesaian pertidaksamaan tersebut sebagai berikut.
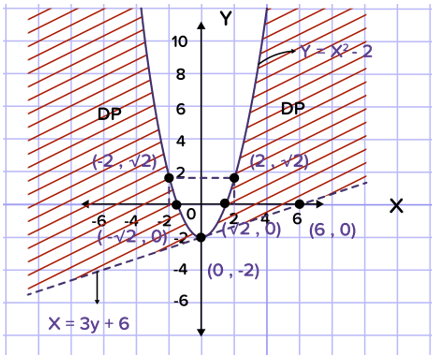
Dengan demikian, gambar grafik penyelesaian sistem pertidaksamaan  seperti pada gambar di atas.
seperti pada gambar di atas.
















