Pertanyaan

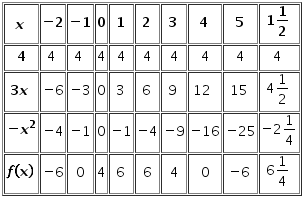
Grafik fungsi y = f ( x ) = 4 + 3 x − x 2 Salinlah tabel berikut dan lengkapi isiannya! Lengkapilah grafik di bawah ini berdasarkan pasangan berurutan ( x , f ( x ) ) pada tabel yang telah kalian lengkapi! Lengkapilah isian berikut berdasarkan grafik yang telah kalian buat! Pembuat nol fungsi adalah x 1 = ... dan x 2 = ... Persamaan sumbu simetri grafik adalah... Koordinat titik balik maksimum adalah ( ... , ... ) Nilai maksimum fungsi adalah.... Daerah hasil fungsi tersebut adalah ... ≤ y ≤ ... , y ∈ R

Grafik fungsi $y = f (x) = 4 + 3 x - x^{2}$

Salinlah tabel berikut dan lengkapi isiannya!

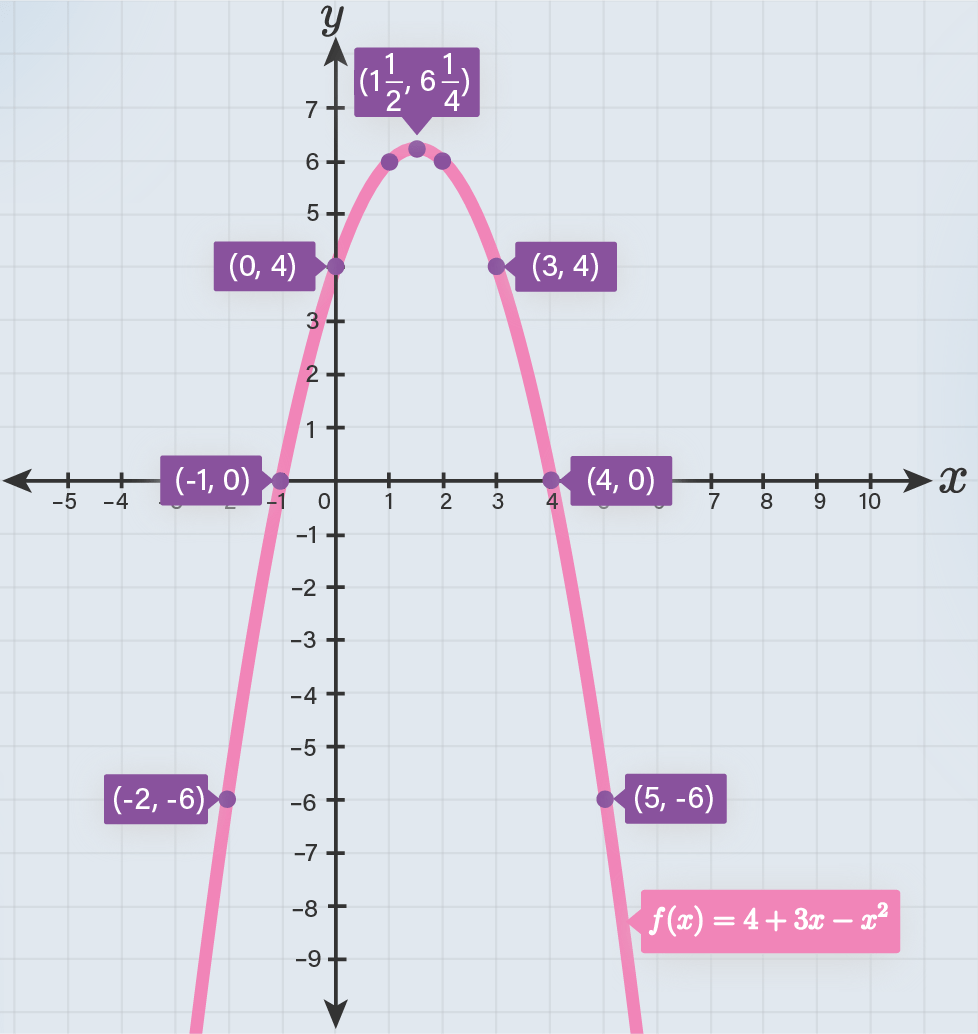
Lengkapilah grafik di bawah ini berdasarkan pasangan berurutan $(x, f (x))$ pada tabel yang telah kalian lengkapi!

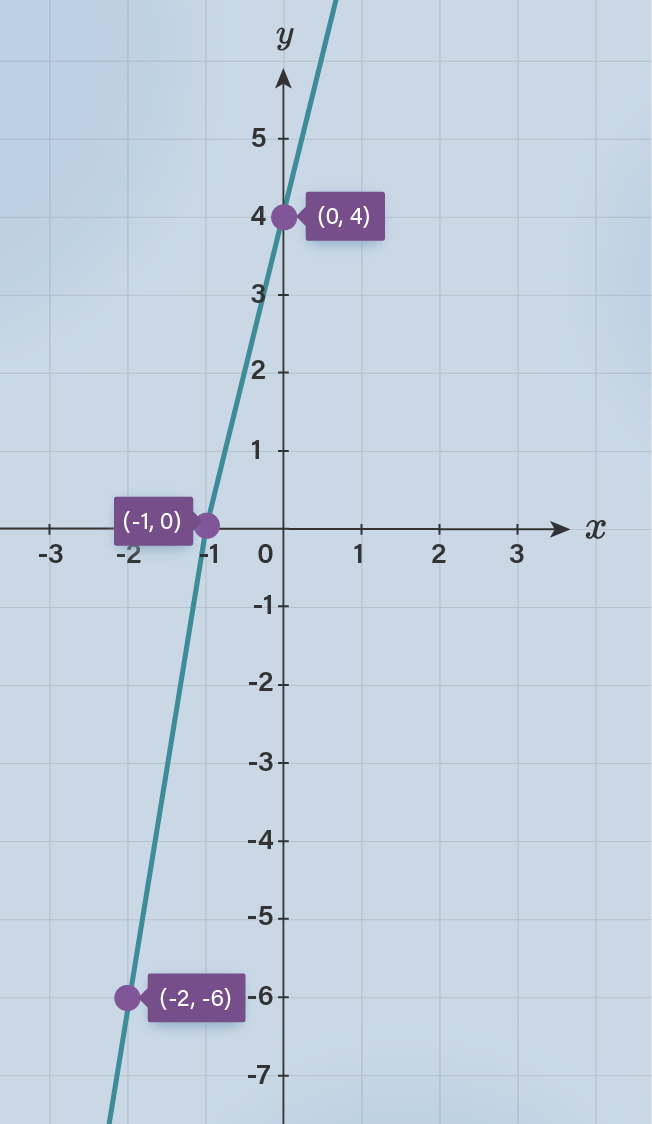
Lengkapilah isian berikut berdasarkan grafik yang telah kalian buat!
- Pembuat nol fungsi adalah $x_{1} = ...$ dan $x_{2} = ...$
- Persamaan sumbu simetri grafik adalah...
- Koordinat titik balik maksimum adalah $(..., ...)$
- Nilai maksimum fungsi adalah....
- Daerah hasil fungsi tersebut adalah $... \leq y \leq ..., y \in R$

P. Nur

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang dimaksud seperti yang telah disebutkan di atas.

Pembahasan

Salinlah tabel berikut dan lengkapi isiannya! Lengkapilah grafik di bawah ini berdasarkan pasangan berurutan ( x , f ( x ) ) pada tabel yang telah kalian lengkapi! Pembuat nol fungsi adalah x 1 = − 1 dan x 2 = 4 . Persamaan sumbu simetri grafik adalah x = 1 2 1 . Koordinat titik balik maksimum adalah ( 1 2 1 , 6 4 1 ) . Nilai maksimum fungsi adalah 6 4 1 . Daerah hasil fungsi tersebut adalah − 6 ≤ y ≤ 6 4 1 , y ∈ R . Dengan demikian, jawaban yang dimaksud seperti yang telah disebutkan di atas.

Salinlah tabel berikut dan lengkapi isiannya!

Lengkapilah grafik di bawah ini berdasarkan pasangan berurutan $(x, f (x))$ pada tabel yang telah kalian lengkapi!

Pembuat nol fungsi adalah $x_{1} = - 1$ dan $x_{2} = 4$ .
Persamaan sumbu simetri grafik adalah $x = 1 \frac{1}{2}$ .
Koordinat titik balik maksimum adalah $(1 \frac{1}{2}, 6 \frac{1}{4})$ .
Nilai maksimum fungsi adalah $6 \frac{1}{4}$ .
Daerah hasil fungsi tersebut adalah $- 6 \leq y \leq 6 \frac{1}{4}, y \in R$ .

Dengan demikian, jawaban yang dimaksud seperti yang telah disebutkan di atas.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (8 rating)

Salsa agustina

Pembahasan lengkap banget

Salwa Aqila

Makasih ❤️

Pertanyaan serupa

Diketahui fungsi f ( x ) = − x 2 − 2 x + 15 , tentukan: a. Titik potong sumbu x b. Titik potong sumbu y c. Sumbu simetri d. Nilai maksimum/minimumnya e. Gambarlah grafik fungsi kuadrat ...

3.6

Jawaban terverifikasi

Diketahui fungsi f ( x ) = 6 + x − x 2 dengan daerah asal − 3 ≤ x ≤ 4 , x ∈ R . a. Gambarlah grafik fungsi y = f ( x ) pada bidang koordinat! b. Tentukan persamaan sumbu simetrinya! c. Tentuk...

4.6

Jawaban terverifikasi

Gambarlah grafik fungsi kuadrat berikut dengan x ∈ R ( bilangan real ) ! c. f ( x ) = ( x + 5 ) 2 + 2 .

170

5.0

Jawaban terverifikasi

Fungsi f ( x ) = x 2 − 9 x + 18 memiliki daerah asal 2 ≤ x ≤ 7 , x ∈ R ( bilangan real ) . a. Buatlah tabelhubungan nilai x dan f ( x ) ! b. Gambarlah grafik f ( x ) = x 2 − 9 x + 18 ! c. Tentukan ...

4.5

Jawaban terverifikasi

Sebuah persegi panjang berukuran panjang x cm dan Iebar ( 8 − x ) cm . L(x) menyatakan fungsi untuk luas persegi panjang tersebut. a. Buatlah model matematika untuk L(x) ! b. Buatlah sketsa grafik...

4.3

Jawaban terverifikasi