Pertanyaan

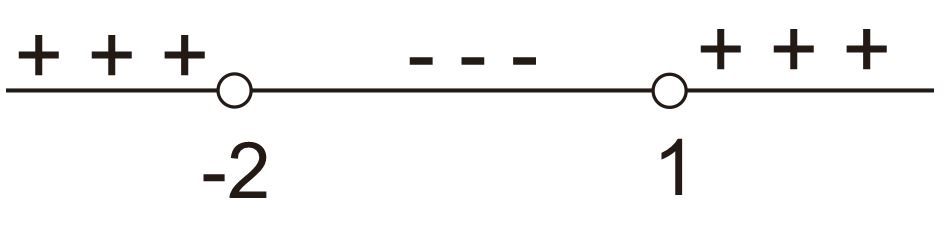
Grafik fungsi y = x 4 + 4 x 3 − 16 x + 1 akan turun pada interval....

Grafik fungsi $y = x^{4} + 4 x^{3} - 16 x + 1$ akan turun pada interval....

M. Nasrullah

Master Teacher

Mahasiswa/Alumni Universitas Negeri Makassar

Jawaban terverifikasi

Jawaban

grafik fungsi akan turun pada interval .

grafik fungsi y equals x to the power of 4 plus 4 x cubed minus 16 x plus 1

akan turun pada interval negative 2 less than x less than 1

Pembahasan

Ingat, jika suatu fungsi turun maka memilki syarat: Sehingga, Maka: Kita faktorkan , ingat untuk mefaktorkan suku banyak, maka lihat kita ambil faktor dari konstanta, yaitu maka faktornya: kemudian kita subtitusi faktor tersebut ke persamaan: Untuk merupakan faktor dari Dengan metode horner: Hasil pembagian: Pada garis bilangan: Maka intervalnya Jadi, grafik fungsi akan turun pada interval .

Ingat, jika suatu fungsi turun maka memilki syarat:

f apostrophe left parenthesis x right parenthesis less than 0

Sehingga,

y equals f open parentheses x close parentheses equals x to the power of 4 plus 4 x cubed minus 16 x plus 1 f apostrophe open parentheses x close parentheses equals 4 x cubed plus 12 x squared minus 16

Maka:

table attributes columnalign right center left columnspacing 0px end attributes row cell f apostrophe left parenthesis x right parenthesis end cell less than 0 row cell 4 x cubed plus 12 x squared minus 16 end cell less than 0 row cell x cubed plus 3 x squared minus 4 end cell less than 0 end table

Kita faktorkan Error converting from MathML to accessible text. , ingat untuk mefaktorkan suku banyak, maka lihat kita ambil faktor dari konstanta, yaitu negative 4 maka faktornya: negative 1 comma space 1 comma space 4 comma space minus 4 comma space 2 comma space minus 2 kemudian kita subtitusi faktor tersebut ke persamaan:

Untuk x equals 1

x equals 1 merupakan faktor dari x squared plus 3 x squared minus 4

Dengan metode horner:

table row 1 1 3 0 cell negative 4 end cell row blank blank 1 4 4 row blank 1 4 4 0 end table

Hasil pembagian:

table attributes columnalign right center left columnspacing 0px end attributes row cell x squared plus 4 x plus 4 end cell equals 0 row cell open parentheses x plus 2 close parentheses open parentheses x plus 2 close parentheses end cell equals 0 row x equals cell negative 2 end cell end table

Pada garis bilangan: