Gambar berikut menunjukkan ABCD adalah segi empat tali busur. ( A , B , C , dan D terletak pada keliling lingkaran) . c. Buktikanlah bahwa △EDA dan △EBC sebangun.

Pembahasan

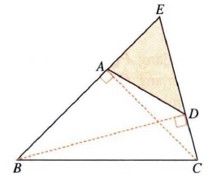
Jawaban yang benar untuk pertanyaan tersebut adalah △EDA sebangun dengan △EBC karena dua pasang sudut yang bersesuaian sama besar yakni ∠ AED=∠BEC , ∠EBC=∠EDA dan ∠BCD=∠EAD . Ingat! Syarat dua segitiga dikatakan sebangun apabila sisi-sisi yang bersesuaian memiliki perbandingan yang sama atau sudut-sudut yang bersesuaian memiliki besar yang sama. Jumlah sudut-sudut yang berhadapan pada segi empat tali busur adalah 18 0 ∘ . Dua sudutdikatakanberpelurusjikajumlah sudutnya 18 0 ∘ . 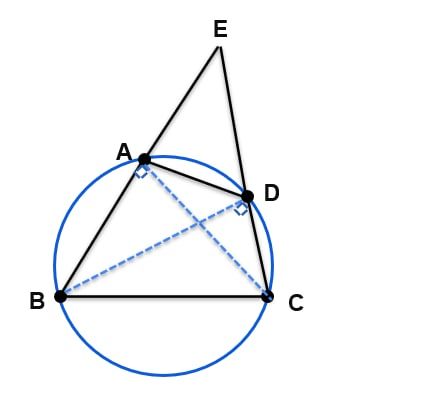Karena ∠ AED dan ∠ BEC berimpit, maka ∠ AED=∠BEC Akan dibuktikan bahwa ∠ EBC = ∠ EDA ∠ ADC dan ∠ EBC merupakan sudut-sudut yang saling berhadapan pada segiempat tali busur ABCD sehingga ∠ ADC + ∠ EBC = 18 0 ∘ . ∠ ADC + ∠ EBC ∠ ADB + ∠ BDC + ∠ EBC ∠ ADB + 9 0 ∘ + ∠ EBC ∠ ADB + ∠ EBC ∠ ADB + ∠ EBC ∠ EBC ​ = = = = = = ​ 18 0 ∘ 18 0 ∘ 18 0 ∘ 18 0 ∘ − 9 0 ∘ 9 0 ∘ 9 0 ∘ − ∠ ADB..............(1) ​ ∠ EDA dan ∠ CDA merupakan sudut yang saling berpelurus sehingga ∠ EDA + ∠ CDA= 18 0 ∘ . ∠ EDA + ∠ CDA ∠ EDA + ∠ BDC + ∠ ADB ∠ EDA + 9 0 ∘ + ∠ ADB ∠ EDA + ∠ ADB ∠ EDA + ∠ ADB ∠ EDA ​ = = = = = = ​ 18 0 ∘ 18 0 ∘ 18 0 ∘ 18 0 ∘ − 9 0 ∘ 9 0 ∘ 9 0 ∘ − ∠ ADB...............(2) ​ Berdasarkan persamaan 1 dan persamaan 2 maka terbukti ∠ EBC = ∠ EDA . Akan dibuktikan bahwa ∠ BCD = ∠ EAD ∠ BAD dan ∠ BCD merupakan sudut-sudut yang saling berhadapan pada segiempat tali busur ABCD sehingga ∠ BAD + ∠ BCD = 18 0 ∘ . ∠ BAD + ∠ BCD ∠ BAC + ∠ CAD + ∠ BCD 9 0 ∘ + ∠ CAD + ∠ BCD ∠ CAD + ∠ BCD ∠ CAD + ∠ BCD ∠ BCD ​ = = = = = = ​ 18 0 ∘ 18 0 ∘ 18 0 ∘ 18 0 ∘ − 9 0 ∘ 9 0 ∘ 9 0 ∘ − ∠ CAD..............(1) ​ ∠ BAD dan ∠ EAD merupakan sudut yang saling berpelurus sehingga ∠ BAD + ∠ EAD= 18 0 ∘ . ∠ BAD + ∠ EAD ∠ BAC + ∠ CAD + ∠ EAD 9 0 ∘ + ∠ CAD + ∠ EAD ∠ CAD + ∠ EAD ∠ CAD + ∠ EAD ∠ EAD ​ = = = = = = ​ 18 0 ∘ 18 0 ∘ 18 0 ∘ 18 0 ∘ − 9 0 ∘ 9 0 ∘ 9 0 ∘ − ∠ CAD...............(2) ​ Berdasarkan persamaan 1 dan persamaan 2 maka terbukti ∠ BCD = ∠ EAD . Dengan demikian,karena dua pasang sudut yang bersesuaian sama besar yakni ∠ AED=∠BEC , ∠EBC=∠EDA dan ∠BCD=∠EAD maka terbukti bahwa △EDA sebangun dengan △EBC .