Pertanyaan

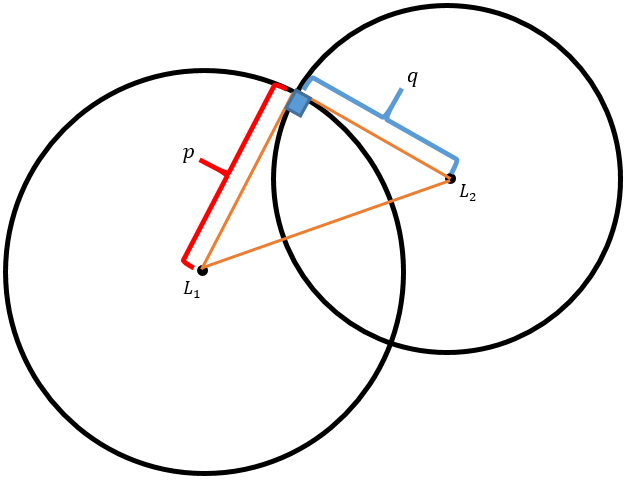
Dua buah lingkaran yang jari-jarinya p cm dan q cm berpotongan dengan sudut siku-siku. Buktikanlah bahwa jarak sentralnya p 2 + q 2 . Catatan: Dua buah lingkaran berpotongandengan sudut siku-siku disebut "dua lingkaranortogonal".

Dua buah lingkaran yang jari-jarinya $p cm$ dan $q cm$ berpotongan dengan sudut siku-siku. Buktikanlah bahwa jarak sentralnya $p^{2} + q^{2}$ .

Catatan: Dua buah lingkaran berpotongan dengan sudut siku-siku disebut "dua lingkaran ortogonal".

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Z. Apriani

Master Teacher

Mahasiswa/Alumni Institut Teknologi Bandung

Jawaban terverifikasi

Jawaban

jarak sentralnya terbukti sama dengan p 2 + q 2 .

jarak sentralnya terbukti sama dengan

p^{2} + q^{2}

Pembahasan

Ingat bahwa syarat dua lingkaran berpotongan berikut: r 1 − r 2 < L 1 L 2 < r 1 + r 2 Diketahui: jari-jarinya p cm dan q cm . berpotongan dengan sudut siku-siku. Berdasarkan syarat dan informasinya, maka perpotongan dua lingkaran tersebut dapat digambarkan sebagai berikut: Sehingga jarak sentralnya adalah sebagai berikut: ( L 1 L 2 ) 2 L 1 L 2 = = = = r L 1 2 + r L 2 2 − 2 ⋅ r L 1 ⋅ r L 2 ⋅ cos 9 0 ∘ p 2 + q 2 − 2 ⋅ p ⋅ q ⋅ 0 p 2 + q 2 p 2 + q 2 Dengan demikian, jarak sentralnya terbukti sama dengan p 2 + q 2 .

Ingat bahwa syarat dua lingkaran berpotongan berikut:

$r_{1} - r_{2} < L_{1} L_{2} < r_{1} + r_{2}$

Diketahui:

jari-jarinya $p cm$ dan $q cm$ .
berpotongan dengan sudut siku-siku.

Berdasarkan syarat dan informasinya, maka perpotongan dua lingkaran tersebut dapat digambarkan sebagai berikut:

Sehingga jarak sentralnya adalah sebagai berikut:

$(L_{1} L_{2})^{2} L_{1} L_{2} = = = = r_{L_{1}}^{2} + r_{L_{2}}^{2} - 2 \cdot r_{L_{1}} \cdot r_{L_{2}} \cdot cos 9 0^{\circ} p^{2} + q^{2} - 2 \cdot p \cdot q \cdot 0 p^{2} + q^{2} p^{2} + q^{2}$

Dengan demikian, jarak sentralnya terbukti sama dengan $p^{2} + q^{2}$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Diketahui persamaan lingkaran L 1 : x 2 + y 2 + 4 x − 6 y + 13 = 0 dan L 2 : x 2 + y 2 − 2 x − 6 y + k = 0 .Tentukan nilai k agar kedua lingkaran tersebut tegak lurus.

5.0

Jawaban terverifikasi

Diketahui dua lingkaran L 1 : x 2 + y 2 − 12 y − 2 y + 1 = 0 dan L 2 : x 2 + y 2 + 4 x + 10 y − 35 = 0 . Periksa apakah kedua lingkaran tersebut beririsan tegak lurus atau tidak?

5.0

Jawaban terverifikasi

Persamaan lingkaran yang memotong lingkaran lain x 2 + y 2 + 2 x + y − 11 = 0 secara tegak lurus dan melalui titik ( 4 , 3 ) , serta pusatnya pada garis 9 x + 4 y = 37 adalah ....

5.0

Jawaban terverifikasi

Di antara empat lingkaran berikut ini, lingkaran yang saling tegak lurus adalah .... L 1 : x 2 + y 2 + 4 x + 2 y + 4 = 0 L 2 : x 2 + y 2 − 8 x − 10 y + 32 = 0 L 3 : x 2 + y 2 − 6 x + 4 y − 12...

5.0

Jawaban terverifikasi

Persamaan lingkaran yang memotong lingkaran lain x 2 + y 2 + 2 x + y − 11 = 0 secara tegak lurus dan melalui titik ( 4 , 3 ) , serta pusatnya pada garis 9 x + 4 y = 37 adalah ....

5.0

Jawaban terverifikasi