Pertanyaan

Dua buah bangun di bawah ini sebangun. Hitunglah: a.Panjang EF, HG, AD, DC

Dua buah bangun di bawah ini sebangun.

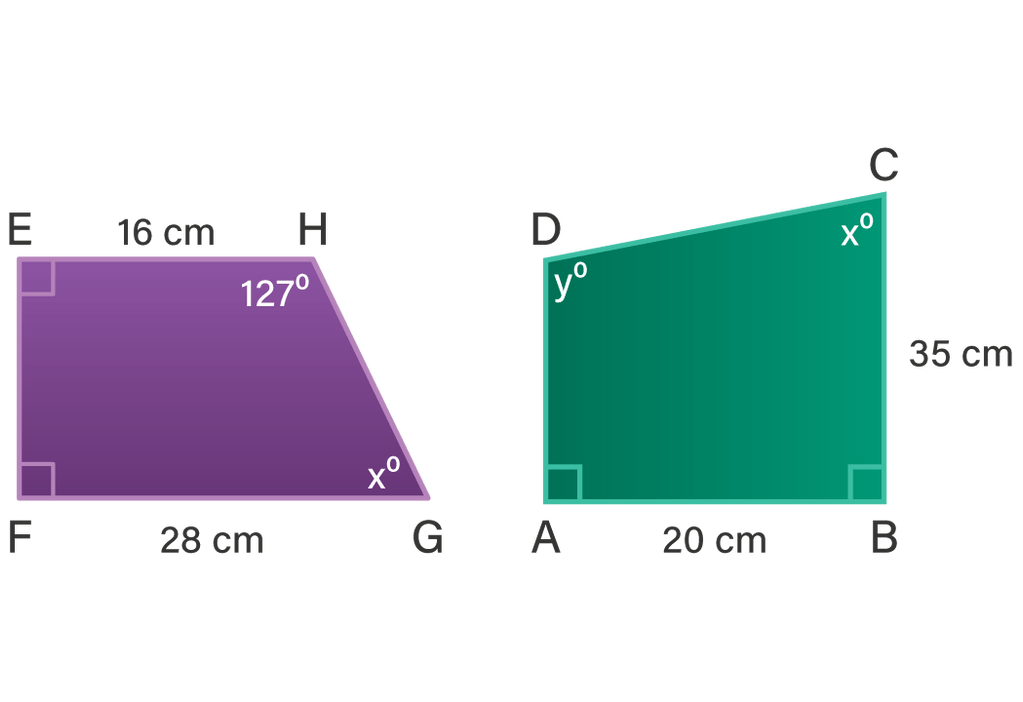
Hitunglah:

a. Panjang EF, HG, AD, DC

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

P. Anggrayni

Master Teacher

Jawaban terverifikasi

Jawaban

panjang , , , dan DC=25cm .

panjang

, dan

DC=25 cm

Pembahasan

Dua atau lebih bangun dikatakan sebangun apabila memenuhi syarat-syarat berikut. 1. Sudut-sudut yang bersesuaian pada bangun tersebut besarnya sama. 2. Panjang sisi-sisi yang bersesuaian tersebut memiliki perbandingan senilai. Trapesium EFGH dan ABCD sebangun, dengan ∠ ABC = ∠ EFG , ∠ DAB = ∠ HEF , ∠ BCD = ∠ FGH , ∠ ADC = ∠ EHG , sehingga pasangan sisi-sisi bersesuaian adalah AB dan EF , BC dan FG , CD dan HG , AD dan EH . Akibatnya berlaku perbandingan senilai sebagai berikut Panjang dapat ditentukan sebagai berikut. AD EH AD 16 cm AD AD = = = = BC FG 35 5 cm 28 4 cm 4 1 16 4 cm × 5 20 cm Panjang dapat ditentukan sebagai berikut. AB EF 20 cm EF EF EF = = = = BC FG 35 5 cm 28 4 cm 5 1 4 × 20 4 cm 16 cm Panjang dan dapat ditentukan dengan dalil Pythagoras sebagai berikut. HG = = = = = EF 2 + ( FG − EH ) 2 ( 16 cm ) 2 + ( 28 cm − 16 cm ) 2 256 cm 2 + 144 cm 2 400 cm 2 20 cm serta DC = = = = = AB 2 + ( BC − AD ) 2 ( 20 cm ) 2 + ( 35 cm − 20 cm ) 2 400 cm 2 + 225 cm 2 625 cm 2 25 cm Dengan demikian, panjang , , , dan DC=25cm .

Dua atau lebih bangun dikatakan sebangun apabila memenuhi syarat-syarat berikut.

1. Sudut-sudut yang bersesuaian pada bangun tersebut besarnya sama.

2. Panjang sisi-sisi yang bersesuaian tersebut memiliki perbandingan senilai.

Trapesium EFGH dan ABCD sebangun, dengan

$∠ ABC = ∠ EFG, ∠ DAB = ∠ HEF, ∠ BCD = ∠ FGH, ∠ ADC = ∠ EHG,$

sehingga pasangan sisi-sisi bersesuaian adalah

$AB dan EF, BC dan FG, CD dan HG, AD dan EH .$

Akibatnya berlaku perbandingan senilai sebagai berikut

$fraction numerator text EH end text over denominator text AD end text end fraction equals fraction numerator text HG end text over denominator text CD end text end fraction equals fraction numerator text FG end text over denominator text BC end text end fraction equals fraction numerator text EF end text over denominator text AB end text end fraction$

Panjang text AD end text dapat ditentukan sebagai berikut.

$\frac{EH}{AD} \frac{16 cm}{AD} AD AD = = = = \frac{FG}{BC} \frac{28 ^{4} cm}{35 ^{5} cm} \frac{16 ^{4} cm \times 5}{4 ^{1}} 20 cm$

Panjang text EF end text dapat ditentukan sebagai berikut.

$\frac{EF}{AB} \frac{EF}{20 cm} EF EF = = = = \frac{FG}{BC} \frac{28 ^{4} cm}{35 ^{5} cm} \frac{4 \times 20 ^{4} cm}{5 ^{1}} 16 cm$

Panjang text HG end text dan text DC end text dapat ditentukan dengan dalil Pythagoras sebagai berikut.

$HG = = = = = EF^{2} + (FG - EH)^{2} (16 cm)^{2} + (28 cm - 16 cm)^{2} 256 cm^{2} + 144 cm^{2} 400 cm^{2} 20 cm$

serta

$DC = = = = = AB^{2} + (BC - AD)^{2} (20 cm)^{2} + (35 cm - 20 cm)^{2} 400 cm^{2} + 225 cm^{2} 625 cm^{2} 25 cm$

Dengan demikian, panjang text EF=16 cm end text , text HG=20 cm end text , text AD=20 cm end text , dan $DC=25 cm$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.5 (10 rating)

Redmi Note9

Pembahasan lengkap banget

zea

cari panjang x, y, dan z

Putri May

Makasih ❤️

Pertanyaan serupa

Perhatikan sketsa gambar berikut! Sebuah foto yang berukuran alasnya 40 cm dan tingginya 60 cm , dipasang pada sebuah karton sehingga lebar karton di sebelah kiri, kanan dan atas foto 5 cm . ...

3.9

Jawaban terverifikasi

Suatu persegi panjang yang selisih panjang dan lebarnya 5 cm adalah sebangun dengan persegi panjang yang selisih antara panjang dan lebarnya 7 , 5 cm . Jika keliling persegi yang kecil 26 cm , maka te...

0.0

Jawaban terverifikasi

Perhatikan gambar di atas! Jika BC = 6 cm dan AC = 10 cm , tentukan keliling persegi PQRB !

5.0

Jawaban terverifikasi

Perhatikan gambar di bawah ini! Jika △ ABC sebangun dengan △ PQR , panjang PR adalah ....

4.3

Jawaban terverifikasi

Diberikan △ ABE dengan AB = 20 cm , AE = 12 cm , dan CE = 6 cm . Panjang CD adalah ....

4.7

Jawaban terverifikasi