Iklan
Pertanyaan
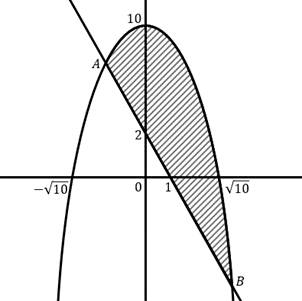
Diketahui R adalah daerah yang dibatasi oleh kurva y = 10 − x 2 dan 2 x + y − 2 = 0 .Dibuat garis y = k sedemikian sehingga daerah R terbagi menjadi dua bagian yang luasnya sama. Luas daerah R yang berada di bawah garis adalah ... satuan luas.
Diketahui adalah ... satuan luas.
16
18
32
36
64
Iklan
DN
D. Natalia
Master Teacher
Jawaban terverifikasi
1
0.0 (0 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia