Pertanyaan

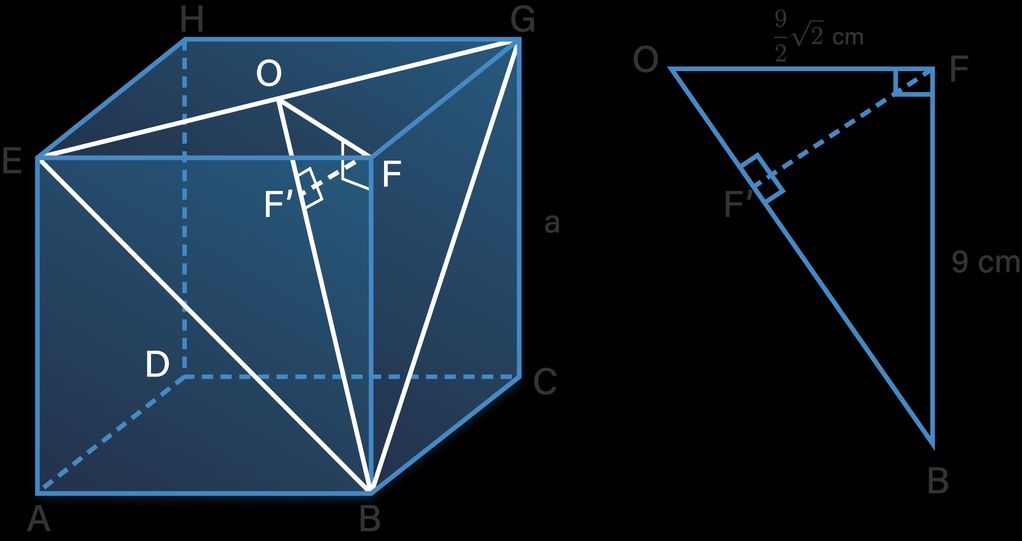
Diketahui kubus ABCD.EFGH dengan panjang rusuk 9 cm . Buat ilustrasi kubus tersebut. Tentukan langkah menentukan jarak titik F ke bidang BEG. Kemudian hitunglah jarak titik F ke bidang BEG.

Diketahui kubus ABCD.EFGH dengan panjang rusuk $9 cm$ . Buat ilustrasi kubus tersebut. Tentukan langkah menentukan jarak titik F ke bidang BEG. Kemudian hitunglah jarak titik F ke bidang BEG.

I. Sutiawan

Master Teacher

Mahasiswa/Alumni Universitas Pasundan

Jawaban terverifikasi

Jawaban

jarak titik F ke bidang BEG adalah .

jarak titik F ke bidang BEG adalah

table attributes columnalign right center left columnspacing 0px end attributes row blank blank 3 end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cell square root of 3 end cell end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank space end table table attributes columnalign right center left columnspacing 0px end attributes row blank blank cm end table

Pembahasan

Ingat! Jarak titik ke bidang adalah lintasan terpendek yang menghubungkan titik dan tegak lurus terhadap bidang. Pada segitiga siku-siku berlaku teorema Pythagoras dengan adalah sisi siku-siku dan sisi miring. Jika dalam suatu segitiga terdapat 2 garis yang dapat dijadikan tinggi ( dan ) dan 2 garis yang dapat dijadikan alas ( dan ), maka berlaku . FH merupakan diagonal bidang kubus, sehingga maka . Perhatikan segitiga BOF siku-siku di F sehingga berlaku teorema Pythagoras sebagai berikut: JarakF ke bidang BEG adalah FF'. Perhatikan segitiga BOF memiliki 2 sisi yang dapat menjadi tinggi dan 2 sisi yang dapat menjadi alas, sehinggarumus kesamaan luas segitiga, maka: Jadi,jarak titik F ke bidang BEG adalah .

Ingat!

Jarak titik ke bidang adalah lintasan terpendek yang menghubungkan titik dan tegak lurus terhadap bidang.
Pada segitiga siku-siku berlaku teorema Pythagoras dengan adalah sisi siku-siku dan sisi miring.
Jika dalam suatu segitiga terdapat 2 garis yang dapat dijadikan tinggi ( dan ) dan 2 garis yang dapat dijadikan alas ( dan ), maka berlaku $t subscript 2 equals fraction numerator a subscript 1 cross times t subscript 1 over denominator a subscript 2 end fraction$ .

FH merupakan diagonal bidang kubus, sehingga FH equals 9 square root of 2 space cm maka FO equals 1 half FH equals 9 over 2 square root of 2 space cm .

Perhatikan segitiga BOF siku-siku di F sehingga berlaku teorema Pythagoras sebagai berikut:

$table attributes columnalign right center left columnspacing 0px end attributes row BO equals cell square root of FO squared plus BF squared end root end cell row blank equals cell square root of open parentheses 9 over 2 square root of 2 close parentheses squared plus 9 squared end root end cell row blank equals cell square root of 81 over 2 plus 81 end root end cell row blank equals cell square root of 243 over 2 end root end cell row blank equals cell 9 square root of 3 over 2 end root end cell row blank equals cell 9 fraction numerator square root of 3 over denominator square root of 2 end fraction cross times fraction numerator square root of 2 over denominator square root of 2 end fraction end cell row blank equals cell 9 over 2 square root of 6 space cm end cell end table$

Jarak F ke bidang BEG adalah FF'. Perhatikan segitiga BOF memiliki 2 sisi yang dapat menjadi tinggi dan 2 sisi yang dapat menjadi alas, sehingga rumus kesamaan luas segitiga, maka:

$table attributes columnalign right center left columnspacing 0px end attributes row EF equals cell fraction numerator FO cross times BF over denominator BO end fraction end cell row blank equals cell fraction numerator begin display style 9 over 2 end style square root of 2 cross times 9 over denominator begin display style 9 over 2 end style square root of 6 end fraction end cell row blank equals cell fraction numerator 9 square root of 2 over denominator square root of 6 end fraction cross times fraction numerator square root of 6 over denominator square root of 6 end fraction end cell row blank equals cell fraction numerator 9 square root of 12 over denominator 6 end fraction end cell row blank equals cell fraction numerator 18 square root of 3 over denominator 6 end fraction end cell row blank equals cell 3 square root of 3 space cm end cell end table$

Jadi, jarak titik F ke bidang BEG adalah .