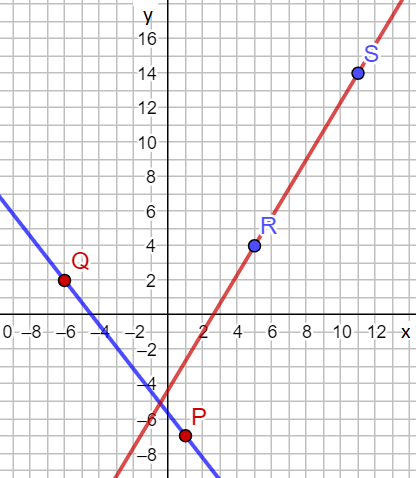
Diketahui garis g melalui titik P ( 1 , − 7 ) dan Q ( − 6 , 2 ) , serta garis h melalui titik R ( 5 , 4 ) dan S ( 11 , 14 ) . a. Hitunglah gradien garis g dan gradien garis h ? b. Bagaimanakah hubungan antara kedua garis tersebut? c. Gambarkanlah garis g dan garis h pada koordinat Cartesius.

Pembahasan

Gradien suatu garis yang melalui titik ( x 1 ​ , y 1 ​ ) dan ( x 2 ​ , y 2 ​ ) dapat ditentukan dengan rumus berikut. m = x 2 ​ − x 1 ​ y 2 ​ − y 1 ​ ​ Dua garis yang saling sejajar memiliki gradien yang sama. Dua garis yang saling tegak lurus dengan gradiennya berturut-turut adalah m h ​ dan m k ​ memiliki hubungan sebagai berikut. m h ​ × m k ​ = − 1 a. Gradien garis g yang melalui titik P ( 1 , − 7 ) dan Q ( − 6 , 2 ) adalah sebagai berikut. m g ​ ​ = = = ​ x 2 ​ − x 1 ​ y 2 ​ − y 1 ​ ​ − 6 − 1 2 − ( − 7 ) ​ − 7 9 ​ ​ Gradien garis h yang melalui titik R ( 5 , 4 ) dan S ( 11 , 14 ) adalah sebagai berikut. m h ​ ​ = = = = ​ x 2 ​ − x 1 ​ y 2 ​ − y 1 ​ ​ 11 − 5 14 − 4 ​ 6 10 ​ 3 5 ​ ​ Dengan demikian, gradien garis m g ​ = − 7 9 ​ dan m h ​ = 3 5 ​ b. Hubungan antara kedua garis dapat ditentukan sebagai berikut. m g ​ − 7 9 ​ ​  =  = ​ m h ​ 3 5 ​ ​ Oleh karena itu, garis g tidak saling sejajar dengangaris h m g ​ ⋅ m h ​ = − 7 9 ​ ⋅ 3 5 ​  = − 1 Oleh karena itu, garis g tidak saling tegak lurus dengangaris h Dengan demikian, dua garis tersebut tidak saling sejajar dan tidak saling tegak lurus, tetapi saling berpotongan. c. Gambargaris g yang melalui titik P ( 1 , − 7 ) dan Q ( − 6 , 2 ) sertagaris h yang melalui titik R ( 5 , 4 ) dan S ( 11 , 14 ) adalah sebagai berikut.