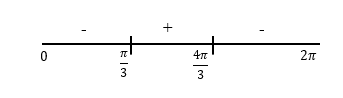Iklan
Pertanyaan
Diketahui fungsi untuk 0 ≤ x ≤ 2 π .Fungsi g naik pada interval ...
Diketahui fungsi untuk . Fungsi naik pada interval ...
Iklan
EL
E. Lestari
Master Teacher
Mahasiswa/Alumni Universitas Sebelas Maret
Jawaban terverifikasi
16
3.8 (11 rating)
AJ
AMAD JUL NAIM
Ini yang aku cari!
DY
DHIVA YULIA PURNANINGTYAS
Jawaban tidak sesuai
NR
Novindra R seiei
Jawaban tidak sesuai
YK
Yeheskiel Kendek
jawabannya salah! Interval fungsi naik dan turun itu harusnya kebalikannya dari jawaban tersebut!
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia