Diketahui bilangan asli p , q , dan r saling relatif prima. Jika q ( p + 1 ) = 42 , 2 r − 3 p = − 3 , dan p ≤ 14 , maka pernyataan yang benar adalah .... (1) Median dari ketiga bilangantersebut adalah 7. (2) Hasil kali bilangan terbesar dan terkecil adalah 30. (3) Rata-rata ketiga bilangan tersebut adalah 5. (4) Selisih dua bilangan terbesar adalah 1.

Pembahasan

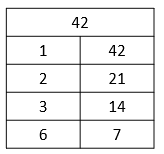
Untuk menentukan nilai dan q terlebih dahulu tentukan faktor-faktor dari 42. Buat tabel perkalian dari 42. Faktor dari 42 adalah 1, 2, 3, 6, 7, 14, 21, dan 42. Ingat bahwa dan q merupakan bilangan asli yang saling relatif prima dengan p ≤ 14 , serta p + 1 dan q merupakan faktor dari 42. Untuk menentukan nilai yang memenuhi perhatikan perhitungan berikut. Untuk p = 1 , maka p + 1 = 2 merupakan faktor dari 42 sehingga p = 1 memenuhi . Untuk p = 2 , maka p + 1 = 3 merupakan faktor dari 42 sehingga p = 2 memenuhi . Untuk p = 3 , maka p + 1 = 4 bukanfaktor dari 42 sehingga p = 3 tidak memenuhi. Untuk p = 4 , maka p + 1 = 5 bukanfaktor dari 42 sehingga p = 4 tidak memenuhi. Untuk p = 5 , maka p + 1 = 6 merupakanfaktor dari 42 sehingga p = 5 memenuhi . Untuk p = 6 , maka p + 1 = 7 merupakanfaktor dari 42 sehingga p = 6 memenuhi . Untuk p = 7 , maka p + 1 = 8 bukanfaktor dari 42 sehingga p = 7 tidak memenuhi. Untuk p = 8 , maka p + 1 = 5 bukanfaktor dari 42 sehingga p = 8 tidak memenuhi. Untuk p = 9 , maka p + 1 = 10 bukanfaktor dari 42 sehingga p = 9 tidak memenuhi. Untuk p = 10 , maka p + 1 = 11 bukanfaktor dari 42 sehingga p = 10 tidak memenuhi. Untuk p = 11 , maka p + 1 = 5 bukanfaktor dari 42 sehingga p = 11 tidak memenuhi. Untuk p = 12 , maka p + 1 = 13 bukanfaktor dari 42 sehingga p = 12 tidak memenuhi. Untuk p = 13 , maka p + 1 = 14 merupakanfaktor dari 42 sehingga p = 13 memenuhi . Untuk p = 14 , maka p + 1 = 15 bukanfaktor dari 42 sehingga p = 14 tidak memenuhi. Dengan demikian, nilai yang memenuhi adalah 1, 2, 5, 6, dan 13. Untuk menentukan nilai q , substitusikan setiap nilai yang memenuhi ke q ( p + 1 ) = 42. Perhatikan perhitungan berikut! Untuk p = 1 , maka akan diperoleh nilai q sebagai berikut. q ( p + 1 ) q ( 1 + 1 ) q ( 2 ) 2 q ( 2 ) ​ q ​ = = = = = ​ 42 42 42 2 42 ​ 21 ​ Karena dan q bilangan asli serta saling relatif prima, maka ( p , q ) = ( 1 , 21 ) memenuhi. Untuk p = 2 , maka akan diperoleh nilai q sebagai berikut.. q ( p + 1 ) q ( 3 ) 3 q ( 3 ) ​ q ​ = = = = ​ 42 42 3 42 ​ 14 ​ Karena dan q bilangan asli serta saling relatif prima, maka ( p , q ) = ( 2 , 14 ) tidak memenuhi. Untuk p = 5 , makamaka akan diperoleh nilai q sebagai berikut.. q ( p + 1 ) q ( 6 ) 6 q ( 6 ) ​ q ​ = = = = ​ 42 42 6 42 ​ 7 ​ Karena dan q bilangan asli serta saling relatif prima, maka ( p , q ) = ( 5 , 7 ) memenuhi. Untuk p = 6 , maka akan diperoleh nilai q sebagai berikut.. q ( p + 1 ) q ( 7 ) 7 q ( 7 ) ​ q ​ = = = = ​ 42 42 7 42 ​ 6 ​ Karena dan q bilangan asli sertasaling relatif prima, maka ( p , q ) = ( 6 , 6 ) tidak memenuhi. Untuk p = 13 , maka akan diperoleh nilai q sebagai berikut.. q ( p + 1 ) q ( 14 ) 14 q ( 14 ) ​ q ​ = = = = ​ 42 42 14 42 ​ 3 ​ Karena dan q bilangan asli sertasaling relatif prima, maka ( p , q ) = ( 13 , 3 ) memenuhi. Kemudian, diketahui pula 2 r − 3 p = − 3 sehingga diperoleh perhitungan sebagai berikut. Untuk p = 1 diperoleh perhitungan sebagai berikut. 2 r − 3 ( 1 ) 2 r − 3 2 r r ​ = = = = ​ − 3 − 3 0 0 ​ Karena dan r bilangan asli serta saling relatif prima, maka ( p , r ) = ( 1 , 0 ) tidak memenuhi. Untuk p = 2 diperoleh perhitungan sebagai berikut. 2 r − 3 ( 2 ) 2 r − 6 2 r r ​ = = = = ​ − 3 − 3 3 2 3 ​ ​ Karena dan r bilangan asli sertasaling relatif prima, maka ( p , r ) = ( 2 , 2 3 ​ ) tidak memenuhi. Untuk p = 5 diperoleh perhitungan sebagai berikut. 2 r − 3 ( 5 ) 2 r − 15 2 r r ​ = = = = ​ − 3 − 3 12 6 ​ Karena dan r bilangan asli sertasaling relatif prima,maka ( p , r ) = ( 5 , 6 ) memenuhi. Untuk p = 6 diperoleh perhitungan sebagai berikut. 2 r − 3 ( 6 ) 2 r − 18 2 r r ​ = = = = ​ − 3 − 3 15 2 15 ​ ​ Karena dan r bilangan asli sertasaling relatif prima,maka ( p , r ) = ( 6 , 2 15 ​ ) tidakmemenuhi. Untuk p = 13 diperoleh perhitungan sebagai berikut. 2 r − 3 ( 13 ) 2 r − 39 2 r r r ​ = = = = = ​ − 3 − 3 36 2 36 ​ 18 ​ Karena dan r bilangan asli sertasaling relatif prima, maka ( p , r ) = ( 13 , 18 ) memenuhi. Oleh karena itu, diperoleh pasangan ( p , q ) dan ( p , r ) adalah sebagai berikut. Untuk ( p , q ) : ( 1 , 21 ) , ( 5 , 7 ) , dan ( 13 , 3 ) . Untuk ( p , r ) : ( 5 , 6 ) dan ( 13 , 18 ) . Dengan demikian, pasangan ( p , q , r ) yang merupakan bilangan asli dan saling relatif prima dengan p ≤ 14 adalah ( 5 , 7 , 6 ) . Selanjutnya, untuk menentukan pernyataan yang benar maka perlu diuraikan satu persatu. Pernyataan (1) : Median dari ketiga bilangantersebut adalah 7. Dari perhitungan diperoleh bahwa p = 5 , q = 7 , dan r = 6. Jika bilangannya diurutkan menjadi 5 , 6 , 7. Karena median adalah nilai tengah dari data terurut, maka median dari ketiga bilangan tersebut adalah 6. Dengan demikian, pernyataan (1) bernilai SALAH . Pernyataan (2) : Hasil kali bilangan terbesar dan terkecil adalah 30. Dari ketiga bilangan, bilangan terkecilnya adalah 5 dan bilangan terbesarnya adalah 7. Hasil kali kedua bilangan tersebut adalah 5 ⋅ 7 = 35. Dengan demikian,pernyataan (2) bernilai SALAH . Pernyataan(3) : Rata-rata ketiga bilangan tersebut adalah 5. Rata-rata ketiga bilangan tersebut adalah sebagai berikut. Rata ‐ rata ​ = = = ​ 3 5 + 7 + 6 ​ 3 18 ​ 6 ​ Dengan demikian,pernyataan (3) bernilai SALAH . Pernyataan(4) :Selisih dua bilangan terbesar adalah 1. Dari perhitungan diperoleh bahwa p = 5 , q = 7 , dan r = 6. Dua bilangan terbesarnya adalah 6 dan 7 sehingga selisih dari kedua bilangan tersebut adalah 7 − 6 = 1. Dengan demikian,pernyataan (4) bernilai BENAR . Dari pernyataan (1), (2), (3), dan (4) yang bernilai benar adalah hanya pernyataan(4). Jadi, jawaban yang tepat adalah D.