Roboguru
SD
SMP
SMA
SBMPTN & UTBK

Diketahui beberapa garis lurus berikut ini. 1. y=12. y=−13. 12x+5y+7=04. 5x−12y+4=0 Dari beberapa garis di atas, yang merupakan garis singgung persekutuan lingkaran  dan lingkaran  adalah ....

Pertanyaan

Diketahui beberapa garis lurus berikut ini.

1. space y equals 1 2. space y equals negative 1 3. space 12 x plus 5 y plus 7 equals 0 4. space 5 x minus 12 y plus 4 equals 0

Dari beberapa garis di atas, yang merupakan garis singgung persekutuan lingkaran straight L subscript 1 colon space open parentheses x minus 2 close parentheses squared plus open parentheses y plus 1 close parentheses squared equals 4 dan lingkaran straight L subscript 2 colon space open parentheses x minus 1 close parentheses squared plus open parentheses y minus 4 close parentheses squared equals 9 adalah ....

  1. 1 dan 3

  2. 2 dan 3

  3. 2 dan 4

  4.  1, 3 dan 4

  5. 2, 3 dan 4

D. Natalia

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah D.

Pembahasan

Perhatikan bahwa pusat dan jari-jari lingkaran straight L subscript 1 colon space open parentheses x minus 2 close parentheses squared plus open parentheses y plus 1 close parentheses squared equals 4 adalah sebagai berikut.

begin mathsize 14px style straight P subscript 1 open parentheses 2 comma negative 1 close parentheses straight r subscript 1 equals square root of 4 equals 2 end style

Kemudian, pusat dan jari-jari lingkaran straight L subscript 2 colon space open parentheses x minus 1 close parentheses squared plus open parentheses y minus 4 close parentheses squared equals 9 adalah sebagai berikut.

straight P subscript 2 open parentheses 1 , space 4 close parentheses straight r subscript 2 equals square root of 9 equals 3

Jika kita gambar di koordinat kartesius, maka posisi kedua lingkaran akan saling bersinggungan.

Misal garis singgung kedua lingkaran di atas adalah y minus m x minus c equals 0.

Jarak titik pusat ke garis singgung akan sama dengan jari-jari dari masing-masing lingkaran. Oleh karena itu, jarak titik begin mathsize 14px style straight P subscript 1 equals open parentheses 2 comma negative 1 close parentheses end style ke garis singgung y minus m x minus c equals 0 akan sama dengan panjang jari-jari straight L subscript 1, serta jarak straight P subscript 2 equals open parentheses 1 , space 4 close parentheses ke garis singgung akan sama dengan panjang jari-jari straight L subscript 2.

Perhatikan perhitungan pada straight L subscript 1 berikut ini!

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator 1 open parentheses negative 1 close parentheses minus m open parentheses 2 close parentheses minus c over denominator square root of open parentheses negative m close parentheses squared plus 1 squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator negative 1 minus 2 m minus c over denominator square root of m squared plus 1 end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator negative open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction end cell equals cell plus-or-minus 2 end cell row cell 1 plus 2 m plus c end cell equals cell plus-or-minus 2 square root of 1 plus m squared end root end cell row c equals cell plus-or-minus 2 square root of 1 plus m squared end root minus open parentheses 1 plus 2 m close parentheses blank horizontal ellipsis blank open parentheses 1 close parentheses end cell end table

Selanjutnya, perhatikan perhitungan pada straight L subscript 2 berikut ini!

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator 1 open parentheses 4 close parentheses minus m open parentheses 1 close parentheses minus c over denominator square root of open parentheses negative m close parentheses squared plus 1 squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of m squared plus 1 end root end fraction close vertical bar end cell equals 3 row cell fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction end cell equals cell plus-or-minus 3 end cell row cell 4 minus m minus c end cell equals cell plus-or-minus 3 square root of 1 plus m squared end root end cell row c equals cell 4 minus m minus-or-plus 3 square root of 1 plus m squared end root blank horizontal ellipsis space open parentheses 2 close parentheses end cell end table

Dari persamaan (1) dan (2) diperoleh hubungan sebagai berikut.

begin mathsize 12px style table attributes columnalign right center left columnspacing 0px end attributes row cell plus-or-minus 2 square root of 1 plus m squared end root minus open parentheses 1 plus 2 m close parentheses end cell equals cell 4 minus m minus minus-or-plus 3 square root of 1 plus m squared end root end cell row cell plus-or-minus 2 square root of 1 plus m squared end root plus-or-minus 3 square root of 1 plus m squared end root end cell equals cell 4 minus m plus open parentheses 1 plus 2 m close parentheses end cell row cell plus-or-minus 2 square root of 1 plus m squared end root plus-or-minus 3 square root of 1 plus m squared end root end cell equals cell 5 plus m end cell end table end style

Perhatikan pada bagian plus-or-minus 2 dan plus-or-minus 3, akan terdapat 4 kemungkinan, yaitu plus-or-minus 5 dan plus-or-minus 1.


Kemungkinan 1.

begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row cell plus-or-minus 5 square root of 1 plus m squared end root end cell equals cell 5 plus m end cell row cell open parentheses plus-or-minus 5 square root of 1 plus m squared end root close parentheses squared end cell equals cell open parentheses 5 plus m close parentheses squared end cell row cell 25 open parentheses 1 plus m squared close parentheses end cell equals cell 25 plus 10 m plus m squared end cell row cell 25 m squared minus m squared minus 10 m plus 25 minus 25 end cell equals 0 row cell 24 m squared minus 10 m end cell equals 0 row cell 2 m open parentheses 12 m minus 5 close parentheses end cell equals 0 row blank blank blank end table end style

Diperoleh nilai m equals 0 atau begin mathsize 14px style m equals 5 over 12 end style.

Kemungkinan nilai c untuk m equals 0 adalah sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row c equals cell plus-or-minus 2 square root of 1 plus m squared end root minus open parentheses 1 plus 2 m close parentheses end cell row blank equals cell plus-or-minus 2 square root of 1 plus 0 squared end root minus open parentheses 1 plus 2 open parentheses 0 close parentheses close parentheses end cell row blank equals cell plus-or-minus 2 open parentheses 1 close parentheses minus 1 end cell row blank equals cell plus-or-minus 2 minus 1 end cell row blank equals cell 1 space atau space minus 3 end cell end table

Kemungkinan nilai c untuk begin mathsize 14px style m equals 5 over 12 end style adalah sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row c equals cell plus-or-minus 2 square root of 1 plus m squared end root minus open parentheses 1 plus 2 m close parentheses end cell row blank equals cell plus-or-minus 2 square root of 1 plus open parentheses 5 over 12 close parentheses squared end root minus open parentheses 1 plus 2 times 5 over 12 close parentheses end cell row blank equals cell plus-or-minus 2 square root of 1 plus 25 over 144 end root minus open parentheses 1 plus 5 over 6 close parentheses end cell row blank equals cell plus-or-minus 2 square root of 169 over 144 end root minus 11 over 6 end cell row blank equals cell plus-or-minus 2 times 13 over 12 minus 11 over 6 end cell row blank equals cell plus-or-minus 13 over 6 minus 11 over 6 end cell row blank equals cell 1 third blank atau blank minus 4 end cell end table

Langkah selanjutnya, cek ke-4 pasangan nilai m dan c ke perhitungan jarak kedua titik pusat ke garis singgung kedua lingkaran, apakah memenuhi atau tidak.

Cek untuk nilai m equals 0 dan c equals 1, didapat perhitungan sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 2 open parentheses 0 close parentheses plus 1 close parentheses over denominator square root of 1 plus 0 squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 0 plus 1 close parentheses over denominator square root of 1 end fraction close vertical bar end cell equals 2 row cell open vertical bar 2 over 1 close vertical bar end cell equals 2 row cell open vertical bar 2 close vertical bar end cell equals cell 2 blank bold left parenthesis bold BENAR bold right parenthesis end cell row blank blank blank row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 minus 0 minus 1 over denominator square root of 1 plus 0 squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar 3 over 1 close vertical bar end cell equals 3 row cell open vertical bar 3 close vertical bar end cell equals cell 3 blank bold left parenthesis bold BENAR bold right parenthesis end cell end table

Karena keduanya benar, maka pasangan nilai m equals 0 dan c equals 1 memenuhi persamaan garis singgung yang diinginkan.

Cek untuk nilai m equals 0 dan c equals negative 3, didapat perhitungan sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 2 open parentheses 0 close parentheses minus 3 close parentheses over denominator square root of 1 plus 0 squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 0 minus 3 close parentheses over denominator square root of 1 end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator negative 2 over denominator 1 end fraction close vertical bar end cell equals 2 row cell open vertical bar negative 2 close vertical bar end cell equals cell 2 blank bold left parenthesis bold BENAR bold right parenthesis end cell row blank blank blank row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 minus 0 minus 3 over denominator square root of 1 plus 0 squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar 1 over 1 close vertical bar end cell equals 3 row cell open vertical bar 1 close vertical bar end cell equals cell 3 blank bold left parenthesis bold SALAH bold right parenthesis end cell end table

Karena hanya salah satu yang benar, maka pasangan nilai m equals 0 dan c equals negative 3 tidak memenuhi persamaan garis singgung yang diinginkan.

Cek untuk nilai m equals 5 over 12 dan c equals 1 third, didapat perhitungan sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 2 open parentheses 5 over 12 close parentheses plus 1 third close parentheses over denominator square root of 1 plus open parentheses 5 over 12 close parentheses squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 5 over 6 plus 1 third close parentheses over denominator square root of 1 plus 25 over 144 end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator 13 over 6 over denominator square root of 169 over 144 end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator 13 over 6 over denominator 13 over 12 end fraction close vertical bar end cell equals 2 row cell open vertical bar 2 close vertical bar end cell equals cell 2 blank open parentheses bold BENAR close parentheses end cell row blank blank blank row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 minus 5 over 12 minus 1 third over denominator square root of 1 plus open parentheses 5 over 12 close parentheses squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 39 over 12 over denominator square root of 1 plus 25 over 144 end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 39 over 12 over denominator square root of 169 over 144 end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 39 over 12 over denominator 13 over 12 end fraction close vertical bar end cell equals 3 row cell open vertical bar 3 close vertical bar end cell equals cell 3 blank open parentheses bold BENAR close parentheses end cell end table

Karena keduanya benar, maka pasangan nilai m equals 5 over 12 dan c equals 1 third memenuhi persamaan garis singgung yang diinginkan.

Cek untuk nilai m equals 5 over 12 dan c equals negative 4, didapat perhitungan sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 2 open parentheses 5 over 12 close parentheses minus 4 close parentheses over denominator square root of 1 plus open parentheses 5 over 12 close parentheses squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 5 over 6 minus 4 close parentheses over denominator square root of 1 plus 25 over 144 end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator negative 13 over 6 over denominator square root of 169 over 144 end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator negative 13 over 6 over denominator 13 over 12 end fraction close vertical bar end cell equals 2 row cell open vertical bar negative 2 close vertical bar end cell equals cell 2 blank bold left parenthesis bold BENAR bold right parenthesis end cell row blank blank blank row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 minus 5 over 12 plus 4 over denominator square root of 1 plus open parentheses 5 over 12 close parentheses squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 8 minus 5 over 12 over denominator square root of 1 plus 25 over 144 end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 91 over 12 over denominator square root of 169 over 144 end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 91 over 12 over denominator 13 over 12 end fraction close vertical bar end cell equals 3 row cell open vertical bar 91 over 13 close vertical bar end cell equals cell 3 blank bold left parenthesis bold SALAH bold right parenthesis end cell end table

Karena hanya salah satu yang benar, maka pasangan nilai m equals 5 over 12 dan c equals negative 4 tidak memenuhi persamaan garis singgung yang diinginkan.

Dari kemungkinan pertama diperoleh dua pasangan nilai m dan c yang memenuhi.

Persamaan garis singgung untuk m equals 0 dan c equals 1 adalah sebagai berikut.

begin mathsize 14px style y equals m x plus c y equals 1 end style

Persamaan garis singgung untuk m equals 5 over 12 dan c equals 1 third adalah sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row y equals cell 5 over 12 x plus 1 third end cell row cell 12 y end cell equals cell 5 x plus 4 end cell end table


Kemungkinan 2.

table attributes columnalign right center left columnspacing 0px end attributes row cell plus-or-minus square root of 1 plus m squared end root end cell equals cell 5 plus m end cell row cell open parentheses plus-or-minus square root of 1 plus m squared end root close parentheses squared end cell equals cell open parentheses 5 plus m close parentheses squared end cell row cell 1 plus m squared end cell equals cell 25 plus 10 m plus m squared end cell row 1 equals cell 10 m plus 25 end cell row cell negative 24 end cell equals cell 10 m end cell row m equals cell negative 24 over 10 end cell row m equals cell negative 12 over 5 end cell end table

Kemungkinan nilai c untuk begin mathsize 14px style m equals negative 12 over 5 end style adalah sebagai berikut.

table attributes columnalign right center left columnspacing 0px end attributes row c equals cell plus-or-minus 2 square root of 1 plus open parentheses negative 12 over 5 close parentheses squared end root minus open parentheses 1 plus 2 open parentheses negative 12 over 5 close parentheses close parentheses end cell row blank equals cell plus-or-minus 2 square root of 1 plus 144 over 25 end root minus open parentheses 1 minus 24 over 5 close parentheses end cell row blank equals cell plus-or-minus 2 square root of 169 over 25 end root minus open parentheses negative 19 over 5 close parentheses end cell row blank equals cell plus-or-minus 2 times 13 over 5 plus 19 over 5 end cell row blank equals cell plus-or-minus 26 over 5 plus 19 over 5 end cell row blank equals cell 9 blank atau space minus 7 over 5 end cell end table


Langkah selanjutnya, cek ke-2 pasangan nilai m dan c ke perhitungan jarak kedua titik pusat ke garis singgung kedua lingkaran, apakah memenuhi atau tidak.

Cek untuk nilai m equals negative 12 over 5 dan c equals 9 pada kedua lingkaran, apakah memenuhi atau tidak.

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 2 open parentheses negative 12 over 5 close parentheses plus 9 close parentheses over denominator square root of 1 plus open parentheses negative 12 over 5 close parentheses squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar 2 close vertical bar end cell equals cell 2 blank begin bold style left parenthesis BENAR right parenthesis end style end cell row blank blank blank row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 plus 12 over 5 minus 9 over denominator square root of 1 plus open parentheses negative 12 over 5 close parentheses squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar negative 1 close vertical bar end cell equals cell 3 blank begin bold style left parenthesis SALAH right parenthesis end style end cell end table

Karena hanya salah satu yang benar, maka pasangan nilai m equals negative 12 over 5 dan c equals 9 tidak memenuhi persamaan garis singgung yang diinginkan.

Cek untuk nilai m equals negative 12 over 5 dan c equals negative 7 over 5 pada kedua lingkaran, apakah memenuhi atau tidak.

table attributes columnalign right center left columnspacing 0px end attributes row cell open vertical bar fraction numerator open parentheses 1 plus 2 m plus c close parentheses over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar fraction numerator open parentheses 1 plus 2 open parentheses negative 12 over 5 close parentheses minus 7 over 5 close parentheses over denominator square root of 1 plus open parentheses negative 12 over 5 close parentheses squared end root end fraction close vertical bar end cell equals 2 row cell open vertical bar 2 close vertical bar end cell equals cell 2 blank begin bold style left parenthesis BENAR right parenthesis end style end cell row blank blank blank row cell open vertical bar fraction numerator 4 minus m minus c over denominator square root of 1 plus m squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar fraction numerator 4 plus 12 over 5 plus 7 over 5 over denominator square root of 1 plus open parentheses negative 12 over 5 close parentheses squared end root end fraction close vertical bar end cell equals 3 row cell open vertical bar 3 close vertical bar end cell equals cell 3 blank begin bold style left parenthesis BENAR right parenthesis end style end cell end table

Karena keduanya benar, maka pasangan nilai m equals negative 12 over 5 dan c equals negative 7 over 5 memenuhi persamaan garis singgung yang diinginkan.

Dari kemungkinan kedua diperoleh pasangan nilai m dan c yang memenuhi adalah m equals negative 12 over 5 dan c equals negative 7 over 5.

Persamaan garis singgung persekutuannya adalah sebagai berikut.

begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row y equals cell m x plus c end cell row y equals cell negative 12 over 5 x minus 7 over 5 end cell row cell 5 y end cell equals cell negative 12 x minus 7 end cell row cell 12 x plus 5 y plus 7 end cell equals 0 end table end style

Dengan demikian, persamaan garis singgung persekutuan dua lingkaran tersebut adalah sebagai berikut.

begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row y equals 1 row cell 12 x plus 5 y plus 7 end cell equals 0 row cell 5 x minus 12 y plus 4 end cell equals 0 end table end style

Jika kita gambar pada koordinat kartesius maka diperoleh gambar berikut ini.

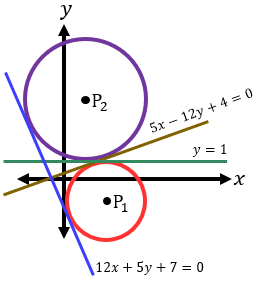
Jadi, jawaban yang tepat adalah D.

14

0.0 (0 rating)

Pertanyaan serupa

Diketahui dua buah persamaan lingkaran sebagai berikut. Banyak persamaan garis singgung yang dapat dibuat dari kedua lingkaran tersebut adalah ….

25

0.0

Jawaban terverifikasi

Diketahui dua buah lingkaran sebagai berikut. Persamaan garis singgung persekutuan yang terbentuk dari kedua lingkaran tersebut adalah ….

92

0.0

Jawaban terverifikasi

Diketahui persamaan lingkaran sebagai berikut. Salah satu persamaan garis singgung persekutuan dua lingkaran di atas adalah ….

39

0.0

Jawaban terverifikasi

Diberikan dua persamaan lingkaran sebagai berikut. L1​: x2+y2−2x−6y+1=0L2​: x2+y2−10x−12y+47=0 Panjang tali busur persekutuan kedua lingkaran tersebut adalah … satuan.

39

0.0

Jawaban terverifikasi

Keliling irisan lingkaran x2+y2=4 dan x2+y2+4x−4y+4=0 adalah ….

158

5.0

Jawaban terverifikasi
Ruangguru

RUANGGURU HQ

Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860

Coba GRATIS Aplikasi Roboguru

Download di Google Play

Coba GRATIS Aplikasi Ruangguru

Download di Google PlayDownload di AppstoreDownload di App Gallery

Produk Ruangguru

Produk Lainnya

  • Brain Academy Online
  • English AcademyBaru
  • Skill Academy
  • Ruangkerja

Bantuan & Panduan

Hubungi Kami

Ruangguru WhatsApp

081578200000

Email info@ruangguru.com

info@ruangguru.com

Contact 02140008000

02140008000

Ikuti Kami

©2022 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia